|
Para qué tantas hipótesis en el Criterio de la Integral.
Luis Alejandro Acuña P.
Escuela de Matemática
Instituto Tecnológico de Costa Rica
Resumen:
Se repasa el planteo tradicional del Criterio de la
Integral para la convergencia de series (con las hipótesis de que la función en
cuestión sea continua, positiva y decreciente, y la conclusión de que la serie y
la integral impropia convergen ambas o divergen ambas). Se muestran ejemplos en
los que fallan una o más de las hipótesis y la conclusión del criterio falla. Se
demuestra que son innecesarias las hipótesis de continuidad y positividad, y
finalmente que basta con una condición aún más débil que la de que la función
sea decreciente. Los resultados se aplican tanto a la equivalencia entre la
convergencia de la serie y la convergencia de la integral impropia como a la
fórmula para la cota del error en las sumas parciales cuando la serie converge.
Palabras Clave: Series infinitas,
criterios de convergencia, continuidad, criterio integral.
Introducción
Al estudiar las series infinitas, uno de los primeros criterios de convergencia que se presentan es el Criterio de la Integral. Su planteo tradicional dice, a grandes rasgos, que si  es una función continua, positiva y decreciente en es una función continua, positiva y decreciente en  , entonces la integral impropia , entonces la integral impropia
 converge si y sólo si la serie converge si y sólo si la serie
 converge. converge.
En este artículo veremos que las hipótesis de continuidad y positividad son innecesarias. Con sólo suponer que  sea decreciente ya se puede demostrar la equivalencia entre las convergencias de la integral y de la serie. Y hay más: resulta que ni siquiera es necesario que sea decreciente ya se puede demostrar la equivalencia entre las convergencias de la integral y de la serie. Y hay más: resulta que ni siquiera es necesario que  sea decreciente. Veremos que hay una condición aún más débil que sigue siendo suficiente en el Criterio de la Integral, pero reservamos los detalles para la última sección. sea decreciente. Veremos que hay una condición aún más débil que sigue siendo suficiente en el Criterio de la Integral, pero reservamos los detalles para la última sección.
Planteo usual del Criterio Integral (CI) en la literatura
Como dijimos, tradicionalmente el enunciado del Criterio de la Integral (CI) pide que la función sea continua, positiva y decreciente. Por ejemplo, Larson, Hostetler y Edwards enuncian en su Cálculo [5]:
Teorema: Si  es positiva, continua y decreciente para es positiva, continua y decreciente para 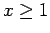 y y 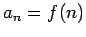 , entonces , entonces
convergen o divergen ambas simultáneamente.
Stewart, en su "Cálculo, trascendentes tempranas'', lo enuncia de manera casi equivalente:
Teorema: Suponga que  es una función continua, positiva y decreciente en es una función continua, positiva y decreciente en  y sea y sea 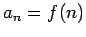 . Entonces la serie . Entonces la serie
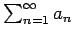 es convergente si y sólo si la integral impropia es convergente si y sólo si la integral impropia
 es convergente. es convergente.
Al menos esa es la manera en que la mayoría de los libros de cálculo lo plantean, incluyendo los textos de Stewart, Larson, Purcell y otros. Curiosamente, los libros de análisis, como los de Apostol, Bartle, Lang o Rudin, omiten la suposición de que  sea continua. Por ejemplo, Rudin, en su libro "Principios de análisis matemático'' [6], enuncia: sea continua. Por ejemplo, Rudin, en su libro "Principios de análisis matemático'' [6], enuncia:
Teorema: Si 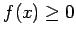 y si y si  es monótona decreciente para es monótona decreciente para 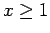 , entonces , entonces
converge, si y sólo si
converge.
Apostol, en su "Análisis matemático'' [2], omite las hipótesis de continuidad y positividad pero añade una nueva, que  tienda a cero: tienda a cero:
Teorema: Sea  una función decreciente definida en una función decreciente definida en 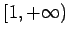 tal que tal que
 . Para . Para  , definimos , definimos
Se tiene entonces:
- i)
 , para , para 
- ii)
 existe. existe.
- iii)
 converge si, y sólo si, la sucesión converge si, y sólo si, la sucesión 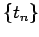 converge. converge.
- iv)
 , para , para 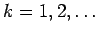
En realidad si  es decreciente y tiende a cero entonces es decreciente y tiende a cero entonces  debe ser positiva, de modo que la hipótesis de positividad, si bien no es explícita, está presente pero escondida en el nuevo planteo. También escondida está la conclusión de que la serie converge si y sólo si la integral converge: el tercer punto del teorema no dice que debe ser positiva, de modo que la hipótesis de positividad, si bien no es explícita, está presente pero escondida en el nuevo planteo. También escondida está la conclusión de que la serie converge si y sólo si la integral converge: el tercer punto del teorema no dice que
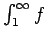 converja sino que la sucesión converja sino que la sucesión
 converge, lo cual es equivalente en presencia de la suposición de que converge, lo cual es equivalente en presencia de la suposición de que  sea positiva. sea positiva.
De cualquier manera, en la práctica las aplicaciones de este teorema no requieren que las condiciones se cumplan particularmente en  : basta con que se cumplan en el intervalo : basta con que se cumplan en el intervalo  , para algún , para algún
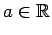 . De manera semejante, la palabra "positiva'' se usa aquí en un sentido no estricto, significando que . De manera semejante, la palabra "positiva'' se usa aquí en un sentido no estricto, significando que 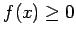 para todo para todo
 . Además, tampoco es necesario que la integral y la serie empiecen en 1; pueden empezar ambas en cualquier . Además, tampoco es necesario que la integral y la serie empiecen en 1; pueden empezar ambas en cualquier
 . .
Definiciones y resultados preliminares
Asegurémonos de que tenemos una base común para lo que sigue. Dos definiciones básicas son:
Definición 1: Si
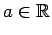 y y
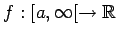 es integrable en cada intervalo es integrable en cada intervalo ![$[a,b]$](img29.gif) , entonces la integral impropia de , entonces la integral impropia de  sobre el intervalo sobre el intervalo  es es
La integral converge si el límite existe, o diverge si no.
Definición 2: Si
 es una sucesión real, su serie es es una sucesión real, su serie es
La serie converge si el límite existe, o diverge si no. La cantidad
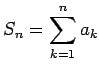 se llama la se llama la 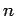 -ésima suma parcial de la serie. -ésima suma parcial de la serie.
Un resultado bien conocido es que cualquier sucesión real monótona y acotada es convergente (Teorema de Bolzano-Weierstrass). Una propiedad semejante se cumple para funciones, y luego necesitaremos los siguientes dos resultados relacionados con esto (sus demostraciones están en el
Apéndice):
Proposición 1: Si 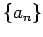 es una sucesión creciente o decreciente, entonces es una sucesión creciente o decreciente, entonces
 respectivamente, donde el supremo podría ser respectivamente, donde el supremo podría ser 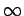 , y el ínfimo , y el ínfimo 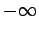 , si la sucesión no es acotada. , si la sucesión no es acotada.
Proposición 2: Si  es creciente o decreciente en es creciente o decreciente en  , entonces , entonces
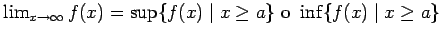 respectivamente, donde el supremo o el ínfimo podría ser respectivamente, donde el supremo o el ínfimo podría ser 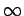 o o 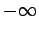 . .
Los siguientes dos resultados son fundamentales. También están demostrados en el
Apéndice.
Proposición 3: Si la serie 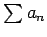 es convergente, entonces es convergente, entonces
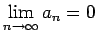 . .
Es tentador pensar que si la integral
 converge entonces converge entonces  debe tender a cero, como sucede con las series. Pero no es así, como veremos en los ejemplos de la siguiente sección. Lo que sí es cierto es: debe tender a cero, como sucede con las series. Pero no es así, como veremos en los ejemplos de la siguiente sección. Lo que sí es cierto es:
Proposición 4: Si la integral
 converge y converge y  es monótona en es monótona en  , entonces , entonces
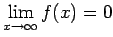 . .
Por último, una propiedad algo más avanzada de las funciones monótonas es que son integrables según Riemann (la definición de integrabilidad se enuncia en el
Apéndice):
Proposición 5: Si  es monótona en es monótona en ![$[a,b]$](img29.gif) , entonces , entonces  es integrable según Riemann en es integrable según Riemann en ![$[a,b]$](img29.gif) . .
Algunos contraejemplos si fallan las hipótesis
Volvamos al Criterio de la Integral y su planteo tradicional (suponiendo que la función es continua, positiva y decreciente). No es difícil encontrar ejemplos en los que fallan esas hipótesis y la integral converge pero la serie diverge, o viceversa. Veamos algunos.
Si falla la continuidad
Considere la función
cuyo gráfico es como el siguiente:

Figura1.
La función  es positiva, pero no continua ni decreciente. La integral es positiva, pero no continua ni decreciente. La integral
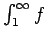 converge porque converge porque
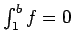 para cualquier para cualquier  , así que , así que
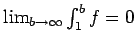 . Pero la serie . Pero la serie
 diverge porque sus sumas parciales son diverge porque sus sumas parciales son
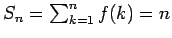 para cualquier para cualquier
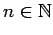 , así que , así que
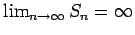 . .
Usando la misma  anterior, ahora la función anterior, ahora la función 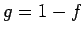 tiene una integral divergente porque tiene una integral divergente porque
 para cualquier para cualquier  , pero su serie converge porque , pero su serie converge porque
 para cualquier para cualquier 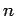 . .
La razón por la que la convergencia de la serie no es equivalente a la convergencia de la integral para las dos funciones anteriores no es que ellas sean discontinuas, sino que no son monótonas. Vea el siguiente ejemplo.
Si falla la monotonía
En el gráfico de la función  anterior es posible conectar los segmentos horizontales con los puntos aislados para construir una función continua con la misma propiedad de anterior es posible conectar los segmentos horizontales con los puntos aislados para construir una función continua con la misma propiedad de  : su integral converge pero su serie diverge. Considere el gráfico siguiente: : su integral converge pero su serie diverge. Considere el gráfico siguiente:
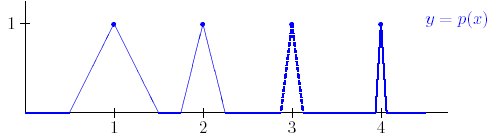
Figura 2.
Llamemos 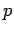 a esta función. Ella es continua, y es constante en cero excepto por un intervalo de ancho 1 centrado en a esta función. Ella es continua, y es constante en cero excepto por un intervalo de ancho 1 centrado en  , un intervalo de ancho , un intervalo de ancho 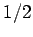 centrado en centrado en 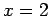 , uno de ancho , uno de ancho  centrado en centrado en 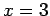 , y así sucesivamente. En cada uno de esos intervalos de ancho , y así sucesivamente. En cada uno de esos intervalos de ancho 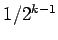 con centro en con centro en 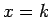 , para , para
 , la integral de , la integral de 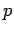 es el área de un triángulo con altura 1 y base es el área de un triángulo con altura 1 y base 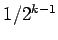 : el área es : el área es 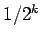 . .
Entonces, para cualquier
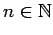 , ,
(la primera desigualdad se debe a que el último triángulo está incompleto). En resumen,
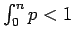 para todo para todo
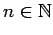 . Por último, como . Por último, como  es una función creciente de es una función creciente de  , y acotada superiormente por 1 como acabamos de ver, resulta (Proposición 2) que , y acotada superiormente por 1 como acabamos de ver, resulta (Proposición 2) que
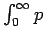 converge. converge.
Por otra parte, es obvio que
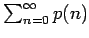 diverge, ya que diverge, ya que  para todo para todo
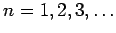 , como la función , como la función  del ejemplo anterior. del ejemplo anterior.
Así es que tenemos una función 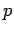 , continua y positiva (pero no decreciente), para la cual la integral converge pero la serie diverge. Tomando, como antes, , continua y positiva (pero no decreciente), para la cual la integral converge pero la serie diverge. Tomando, como antes, 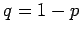 , tendremos un ejemplo de una función continua y positiva tal que su integral diverge, porque , tendremos un ejemplo de una función continua y positiva tal que su integral diverge, porque
pero su serie converge porque
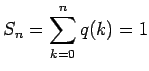 para todo para todo 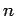 . .
Si falla la positividad
Un ejemplo con una función que no es toda positiva puede ser
 , para , para 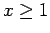 (vea el gráfico abajo). Esta función cambia de signo y tiende a cero de una manera tal que su integral impropia converge, pero (vea el gráfico abajo). Esta función cambia de signo y tiende a cero de una manera tal que su integral impropia converge, pero 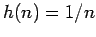 para cada para cada
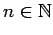 , de modo que la serie , de modo que la serie  diverge (es bien sabido que diverge (es bien sabido que
 , conocida como la serie armónica, diverge). , conocida como la serie armónica, diverge).

Figura 3.
Vamos eliminando las hipótesis
En los cinco ejemplos anteriores las funciones tienen algo en común: ninguna es decreciente. Unas son positivas, una de ellas no; unas son continuas y otras no. Pero ninguna de ellas es decreciente. De las tres hipótesis,  cumple solamente la de positividad y cumple solamente la de positividad y  sólo la de continuidad; sólo la de continuidad; 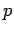 es continua y positiva pero no decreciente. Faltó ver entre los ejemplos una función que fuera sólo decreciente pero no continua o positiva, para la cual convergiera la serie y no la integral, o viceversa. es continua y positiva pero no decreciente. Faltó ver entre los ejemplos una función que fuera sólo decreciente pero no continua o positiva, para la cual convergiera la serie y no la integral, o viceversa.
¿Por qué faltó? Muy sencillo: porque no existe tal función. Pronto demostraremos que cualquier función decreciente, continua o no, positiva o no, satisface la conclusión del Criterio de la Integral.
De hecho, las tres hipótesis tradicionales del CI son innecesarias. Podemos prescindir por completo de las dos primeras y todavía debilitar un poco la tercera, como veremos en esta sección.
¿Es necesaria la continuidad?
La primera hipótesis de la que podemos deshacernos en el CI es la continuidad, a pesar de que los textos usuales de cálculo la incluyen. Tenemos el siguiente lema:
Lema 1: Si  es decreciente y positiva en es decreciente y positiva en  para algún para algún
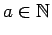 , entonces , entonces
 converge si y sólo si converge si y sólo si
 converge. converge.
La siguiente demostración es típica de lo que puede encontrarse en los libros de análisis matemático.
Demostración: Primero, como  es positiva, tanto es positiva, tanto
 como como
 son funciones crecientes de son funciones crecientes de  y y 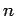 , respectivamente. , respectivamente.
Además, como  es decreciente en es decreciente en  entonces, por una parte, entonces, por una parte,  es integrable en cualquier subintervalo de es integrable en cualquier subintervalo de  (Proposición 5), y por otra, para cualquier entero (Proposición 5), y por otra, para cualquier entero  se tiene se tiene
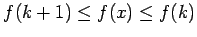 para todo para todo ![$x \in [k,k+1]$](img86.gif) . Integrando los tres términos de la desigualdad sobre el intervalo . Integrando los tres términos de la desigualdad sobre el intervalo ![$[k,k+1]$](img87.gif) obtenemos obtenemos
Sumando ahora para  desde desde  hasta cualquier entero hasta cualquier entero 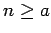 obtenemos obtenemos
o bien
o más simplemente
Supongamos ahora que la integral
 converge. Entonces converge. Entonces
de modo que
La sucesión  es entonces no sólo creciente sino también acotada superiormente, por lo que debe converger (Proposición 1). De ahí que si es entonces no sólo creciente sino también acotada superiormente, por lo que debe converger (Proposición 1). De ahí que si
 converge, también converge, también
 converge. converge.
Recíprocamente, supongamos que la serie
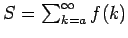 converge. Entonces converge. Entonces
y de ahí que para cualquier real  : :
(donde
 denota la parte entera de denota la parte entera de  ). Entonces la función ). Entonces la función  no sólo es creciente sino también acotada superiormente, y por lo tanto converge (Proposición 2). En conclusión, si no sólo es creciente sino también acotada superiormente, y por lo tanto converge (Proposición 2). En conclusión, si
 converge, converge,
 también converge. también converge.
Terminamos con eso la demostración del Lema 1, sin haber necesitado en ningún momento que  fuera continua. ¿Para qué plantearán esa hipótesis los libros de cálculo? Podría pensarse en una respuesta de tipo didáctico, ya que en los cursos de cálculo el CI se usa casi exclusivamente con funciones continuas. Pero eso no justifica el imponerle al estudiante, cuando resuelve los ejercicios, la carga adicional de verificar una hipótesis completamente innecesaria. fuera continua. ¿Para qué plantearán esa hipótesis los libros de cálculo? Podría pensarse en una respuesta de tipo didáctico, ya que en los cursos de cálculo el CI se usa casi exclusivamente con funciones continuas. Pero eso no justifica el imponerle al estudiante, cuando resuelve los ejercicios, la carga adicional de verificar una hipótesis completamente innecesaria.
¿Es necesario que la función sea positiva?
Resulta que tampoco es necesario suponer que la función sea positiva, aunque muchos textos de análisis sí lo hacen. Partamos solamente de que  es decreciente en es decreciente en  , y consideremos dos posibilidades: , y consideremos dos posibilidades:
No hay ninguna otra posibilidad:  es toda positiva o bien es toda positiva o bien  toma algún valor negativo, y en cualquier caso la integral converge si y sólo si la serie converge. Así de fácil hemos demostrado el siguiente lema, en el que no es necesario que la función sea positiva: toma algún valor negativo, y en cualquier caso la integral converge si y sólo si la serie converge. Así de fácil hemos demostrado el siguiente lema, en el que no es necesario que la función sea positiva:
Lema 2: Si  es decreciente en es decreciente en  para algún para algún
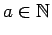 , entonces , entonces
 converge si y sólo si converge si y sólo si
 converge. converge.
¿Y si la función no fuera decreciente?
Incluso esa hipótesis, de que la función sea decreciente, está sobrada hasta cierto punto. Volteando verticalmente el argumento anterior, resulta que si  es creciente entonces el Lema 2 puede aplicarse a es creciente entonces el Lema 2 puede aplicarse a  , que es decreciente: , que es decreciente:
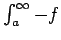 converge si y sólo si converge si y sólo si
 converge. De ahí sigue que, si converge. De ahí sigue que, si  es creciente, es creciente,
Entonces el criterio puede aplicarse ya sea la función creciente o decreciente. Esto implica que hasta la última hipótesis en la formulación tradicional, de que la función sea decreciente, es también prescindible: basta con que  sea monótona. sea monótona.
¿Y la cota del error?
En el planteo tradicional del CI hay un anexo que dice que, bajo las hipótesis del criterio, si la serie y la integral convergen entonces el error en la suma parcial 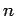 -ésima satisface la desigualdad -ésima satisface la desigualdad
Con la única hipótesis que conservamos aquí, que  sea monótona, también se cumple un resultado casi idéntico. Esto significa que las hipótesis tradicionales del CI no son necesarias ni siquiera para acotar el error, como vemos en este Lema: sea monótona, también se cumple un resultado casi idéntico. Esto significa que las hipótesis tradicionales del CI no son necesarias ni siquiera para acotar el error, como vemos en este Lema:
Lema 3: Si  es monótona en es monótona en  para algún para algún
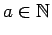 , y la serie , y la serie
 converge, entonces converge, entonces
para cualquier entero 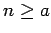 , donde , donde
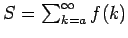 y y
 . .
Demostración: Notemos primero que si la serie converge entonces
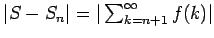 para cualquier para cualquier 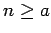 . .
Si  fuera decreciente y tomara algún valor negativo, o si fuera creciente y tomara algún valor positivo, entonces la serie sería divergente como ya notamos, y no habría nada que demostrar. fuera decreciente y tomara algún valor negativo, o si fuera creciente y tomara algún valor positivo, entonces la serie sería divergente como ya notamos, y no habría nada que demostrar.
Supongamos entonces que  es decreciente y positiva en es decreciente y positiva en  . En la demostración del Lema 1 teníamos que, para cualquier . En la demostración del Lema 1 teníamos que, para cualquier 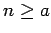 , ,
Si la serie converge (y por ende también la integral), podemos tomar límite cuando 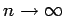 y así obtener y así obtener
Si 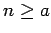 , la desigualdad anterior se aplica también a , la desigualdad anterior se aplica también a 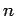 , ya que lo único que se supuso sobre , ya que lo único que se supuso sobre  fue que fue que  era decreciente y positiva en era decreciente y positiva en  , lo cual también es cierto en , lo cual también es cierto en  . Entonces . Entonces
y como supusimos que  era positiva, esa desigualdad es equivalente a era positiva, esa desigualdad es equivalente a
 . .
Por último, si  es más bien creciente y negativa en es más bien creciente y negativa en  , todo lo anterior se aplica a , todo lo anterior se aplica a  en el lugar de en el lugar de  : :
para cualquier 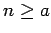 , o bien , o bien
Como  es negativa, la desigualdad anterior equivale también a es negativa, la desigualdad anterior equivale también a
 , con lo que la demostración está completa. , con lo que la demostración está completa.
Conclusión
Para repasar, hicimos lo siguiente: Primero demostramos que si  es decreciente y positiva entonces es decreciente y positiva entonces
 converge si y sólo si converge si y sólo si
 converge. Luego vimos que si converge. Luego vimos que si  es decreciente y toma al menos un valor negativo, entonces tanto la integral como la serie divergen, así que la conclusión se mantiene con la sola hipótesis de que es decreciente y toma al menos un valor negativo, entonces tanto la integral como la serie divergen, así que la conclusión se mantiene con la sola hipótesis de que  sea decreciente y no necesariamente positiva. Lo siguiente fue notar que, si sea decreciente y no necesariamente positiva. Lo siguiente fue notar que, si  es creciente, el criterio anterior se aplica a es creciente, el criterio anterior se aplica a  y por lo tanto también a y por lo tanto también a  , por lo que basta con suponer que , por lo que basta con suponer que  sea monótona. Por último vimos que la cota usual del error se mantiene con esa hipótesis única. sea monótona. Por último vimos que la cota usual del error se mantiene con esa hipótesis única.
En conclusión, luego de haber descartado una por una las hipótesis tradicionales del CI, hemos arribado finalmente a esta versión sumamente austera en sus requisitos:
Teorema (Criterio de la Integral para convergencia de series):
Si  es monótona en es monótona en  para algún para algún
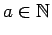 , entonces , entonces
En tal caso,
Apéndice
Aquí demostramos las cinco proposiciones que se enunciaron en la Sección 2, e incluimos las definiciones necesarias para la Proposición 5 acerca de integrabilidad.
Proposición 1: Si 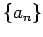 es una sucesión creciente o decreciente, entonces es una sucesión creciente o decreciente, entonces
 respectivamente, donde el supremo podría ser respectivamente, donde el supremo podría ser 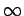 o el ínfimo o el ínfimo 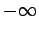 si la sucesión no es acotada. si la sucesión no es acotada.
Demostración: Es muy semejante a la demostración de la Proposición 2, que es más general, por lo que omitimos la presente.
Proposición 2: Si  es creciente o decreciente en es creciente o decreciente en  , entonces , entonces
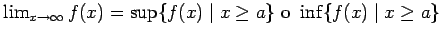 respectivamente, donde el supremo o el ínfimo podría ser respectivamente, donde el supremo o el ínfimo podría ser 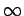 o o 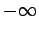 . .
Demostración: Veremos el caso de que  sea decreciente; el otro es análogo. Sea sea decreciente; el otro es análogo. Sea
 . Si . Si  no es acotado inferiormente, para cualquier no es acotado inferiormente, para cualquier
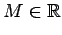 existe algún existe algún  con con 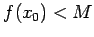 . Entonces . Entonces
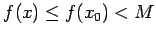 para todo para todo 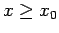 . Esto demuestra que . Esto demuestra que
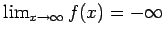 . .
Por otra parte, si 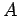 es acotado inferiormente, sea es acotado inferiormente, sea 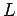 su ínfimo. Para cualquier su ínfimo. Para cualquier 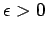 , , 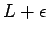 no es cota inferior de no es cota inferior de 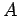 , por lo que existe algún , por lo que existe algún  con con
 . Entonces, para cualquier . Entonces, para cualquier 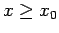 , ,
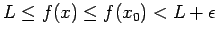 , así que , así que
 para todo para todo 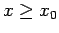 . Esto demuestra que . Esto demuestra que
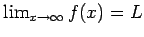 . .
Proposición 3: Si la serie 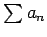 es convergente, entonces es convergente, entonces
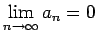 . .
Demostración: Sea
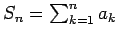 . Como . Como  y y
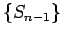 son convergentes (al mismo límite), también lo es su diferencia son convergentes (al mismo límite), también lo es su diferencia
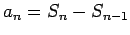 , con , con
 . .
Proposición 4: Si la integral
 converge y converge y  es monótona en es monótona en  , entonces , entonces
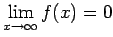 . .
Demostración: Supondremos que  es decreciente (si es decreciente (si  es creciente, el argumento siguiente se aplica a es creciente, el argumento siguiente se aplica a  ). ).
Veamos primero que 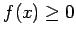 para todo para todo  : Si existiera : Si existiera  con con 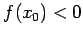 , sería , sería
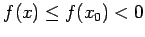 para todo para todo 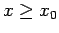 , y entonces, para todo , y entonces, para todo 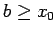 , ,
Cuando  , la expresión a la derecha tendería a , la expresión a la derecha tendería a 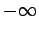 , implicando que , implicando que
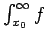 diverge. Esto contradice la hipótesis. diverge. Esto contradice la hipótesis.
Entonces  no es sólo decreciente sino también acotada inferiormente por 0. Por la Proposición 2, existe no es sólo decreciente sino también acotada inferiormente por 0. Por la Proposición 2, existe
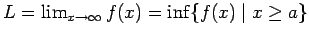 , y debe ser , y debe ser  porque 0 es una cota inferior de porque 0 es una cota inferior de
 . .
Como 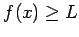 para todo para todo  , entonces para todo , entonces para todo 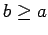
Si fuera 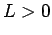 , la expresión a la derecha tendería a , la expresión a la derecha tendería a 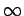 cuando cuando  , como antes implicando que , como antes implicando que
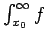 diverge y contradiciendo la hipótesis. diverge y contradiciendo la hipótesis.
En conclusión, 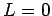 como queríamos probar. como queríamos probar.
Definición 3: Si
![$[a,b] \subset \mathbb{R}$](img160.gif) , una partición , una partición 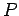 de de ![$[a,b]$](img29.gif) es una sucesión finita es una sucesión finita
![$\conj{x_0, x_1, \ldots, x_n} \subset [a,b]$](img162.gif) con con
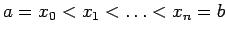 . .
Definición 4: Si  es acotada en es acotada en ![$[a,b]$](img29.gif) y y 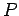 es una partición de es una partición de ![$[a,b]$](img29.gif) , la suma superior de , la suma superior de  para para 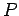 es es
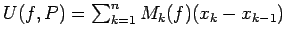 , donde , donde
 . La suma inferior es . La suma inferior es
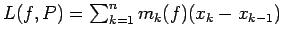 , donde , donde

Definición 5: Si  es acotada en es acotada en ![$[a,b]$](img29.gif) , entonces la integral superior de , entonces la integral superior de  en en ![$[a,b]$](img29.gif) es es
y su integral inferior es
Se dice que  es integrable según Riemann en es integrable según Riemann en ![$[a,b]$](img29.gif) si si
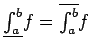 . .
Proposición 5: Si  es monótona en es monótona en ![$[a,b]$](img29.gif) , entonces , entonces  es integrable según Riemann en es integrable según Riemann en ![$[a,b]$](img29.gif) . .
Demostración: Supongamos que  es creciente (el caso de es creciente (el caso de  decreciente es análogo). Para cada decreciente es análogo). Para cada
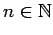 sea sea
 , y sea , y sea  la partición la partición
 . .
Como  es creciente, es creciente,
 , ,
 y y
 para todo para todo 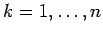 . Entonces . Entonces
y
De ahí que
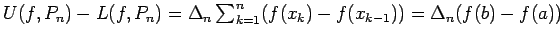 ; es decir, ; es decir,
Finalmente, como
 y y
 , y como obviamente , y como obviamente
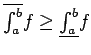 , tenemos , tenemos
Como esta desigualdad se cumple para todo
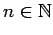 , concluimos que , concluimos que
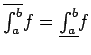 , como queríamos. , como queríamos.
Bibliografía
[1] Apostol, Tom; "Calculus''; 1986.
[2] Apostol, Tom; "Análisis matemático''; 1977.
[3] Bartle, Robert; "Introducción al análisis matemático de una variable''; 2003.
[4] Lang, Serge; "Analysis I''; 1973.
[5] Larson, Roland, Robert Hostetler y Bruce
Edwards; "Cálculo''; 1998.
[6] Rudin, Walter; "Principios de análisis matemático''; 1966.
[7] Stewart, James; "Cálculo. Trascendentes tempranas''; 2001.
Este documento fue generado usando
LaTeX2HTML
translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos, Computer
Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
Revista digital Matemática, Educación e Internet.
Derechos Reservados
|



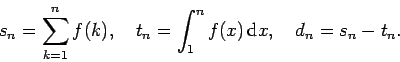
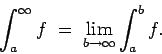
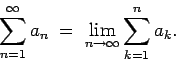
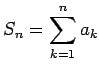 se llama la
se llama la 
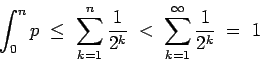
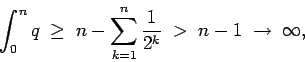
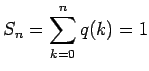 para todo
para todo 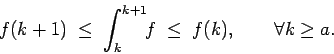

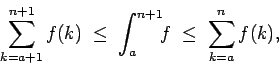
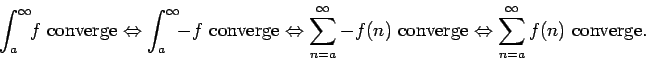
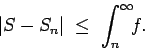

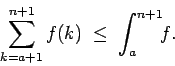
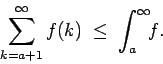
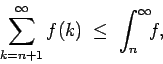



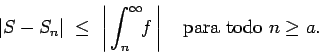
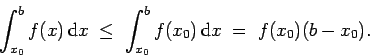

![\begin{displaymath}\overline{\int_a^b}f \; = \; \inf\conj{U(f,P) \mid
\mbox{$P$ es una partición de $[a,b]$}} \end{displaymath}](img168.gif)
![\begin{displaymath}\underline{\int_a^b}f \; = \; \sup\conj{L(f,P) \mid
\mbox{$P$ es una partición de $[a,b]$}}.\end{displaymath}](img169.gif)
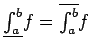 .
.
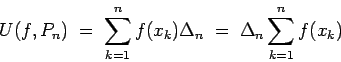


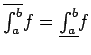 , como queríamos.
, como queríamos.



 y
y
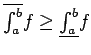 , tenemos
, tenemos