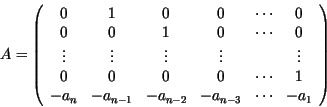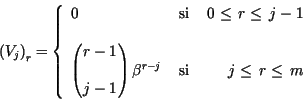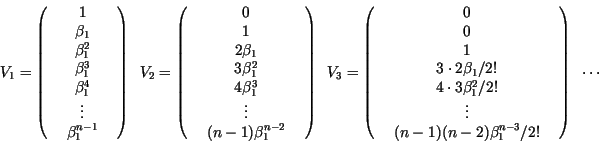| Matrices con entradas enteras e inversa con entradas
enteras
Walter Mora F.
Escuela de Matemática
Instituto Tecnológico de Costa Rica
Resumen
Algunos artículos publicados en The American Mathematical Monthly
discuten acerca de la construcción de matrices con entradas
enteras, valores propios enteros y vectores propios con
componentes enteras, en particular en [1] se hace una
construcción que además permite construir, de manera sencilla,
matrices con entradas enteras cuya inversa también tiene
entradas enteras. En este artículo trata de estas últimas
construcciones e incluye software en Java para generar y
modificar ejemplos y para hacer operaciones de cálculo
de la inversa de una matriz.
Palabras clave: Matrices, inversas, vectores y
valores propios, operaciones elementales,matrices elementales, software didáctico, applet, Java.
Introducción:
Cuando se introducen las matrices en los cursos de álgebra
lineal es a menudo conveniente dar ejemplos numericamente
simples, para centrarse en el manejo de conceptos. Por esto es
veces deseable operar con números enteros y poco con fracciones,
para evitar equivocaciones de índole operacioneal. En este
artículo vamos a dar unas cuantas recetas, siguiendo [1], de
cómo obtener
una buena variedad de ejemplos y de cómo modificarlos.
Construcción:
Consideremos un polinomio
 con con
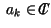 . La matriz . La matriz
es llamada la matriz compañera de 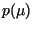 y se tiene que y se tiene que
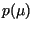 es el polinomio característico de es el polinomio característico de
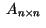 y también su
polinomio mínimo.
y también su
polinomio mínimo.
consideremos los 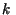 valores propios (complejos) valores propios (complejos)
 de de  con
multiplicidad con
multiplicidad
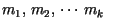 respectivamente. Supongamos que respectivamente. Supongamos que
Para cada 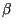 de multiplicidad de multiplicidad  se definen se definen  vectores columna
vectores columna
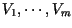 de la siguiente forma de la siguiente forma
Al conjunto
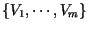 se le llama Cadena de
Jordan asociada a se le llama Cadena de
Jordan asociada a 
Por ejemplo, para 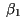 tendríamos tendríamos  vectores columna vectores columna
Para cada valor propio  , ,
 . Se tiene por tanto . Se tiene por tanto
y para
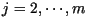
Finalmente, se tiene
Teorema:
Sea
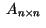 es una matriz compañera
con valores propios es una matriz compañera
con valores propios
 con
multiplicidad algebraica con
multiplicidad algebraica
 respectivamente. Sea
respectivamente. Sea
 la cadena de
Jordan asociada a la cadena de
Jordan asociada a  , ,
 la cadena de Jordan asociada a
la cadena de Jordan asociada a 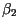 ,y así sucesivamente
hasta llegar a ,y así sucesivamente
hasta llegar a  . Entonces para la matriz . Entonces para la matriz
 se cumple se cumple
| a.) |
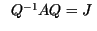 donde donde 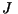 es la forma canónica de
Jordan de es la forma canónica de
Jordan de
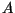 . .
|
| b.) |
Si 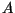 solo tiene los valores propios enteros solo tiene los valores propios enteros
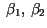 y además estos valores propios
difieren en y además estos valores propios
difieren en  , entonces , entonces 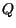 y su inversa tienen entradas
enteras y su inversa tienen entradas
enteras
|
Observemos que si tomamos los  's enteros y los 's enteros y los 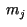 's
enteros y positivos, entonces podemos determinar la matriz
compañera 's
enteros y positivos, entonces podemos determinar la matriz
compañera 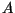 , siguiendo la construcción inicial, y , siguiendo la construcción inicial, y 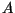 tendría
entradas enteras y valores y vectores propios enteros.
tendría
entradas enteras y valores y vectores propios enteros.
Modificar con operaciones elementales:
Si 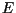 se obtiene de se obtiene de 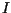 por medio de la operación elemental por medio de la operación elemental
 (La barra indica que se modifica la fila (La barra indica que se modifica la fila
 ), es decir, ), es decir,
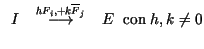 , entonces
la matriz elemental , entonces
la matriz elemental 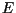 sería de la forma sería de la forma
(si 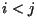 ). Además, en este caso ). Además, en este caso
Como se ve, si  entonces entonces 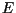 y su inversa tendrían
entradas enteras. y su inversa tendrían
entradas enteras.
Se sabe que si
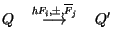 entonces entonces

De ahí que, una vez construida 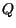 (con entradas enteras), se
pueden aplicar a (con entradas enteras), se
pueden aplicar a 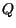 operaciones elementales de la forma operaciones elementales de la forma

y la matriz resultante
tendrá
entradas enteras y también inversa con entradas enteras.
En particular si ponemos  y si y si
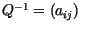 entonces
entonces  se obtiene modificando la columna se obtiene modificando la columna  y
la columna y
la columna  de de 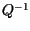
Ejemplos:
- En el caso
 , los dos valores propios deberán
tener multiplicidad , los dos valores propios deberán
tener multiplicidad 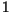 , si ponemos , si ponemos
 y y
 entonces entonces
- En el caso
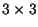 , uno de los valores propios deberá
tener multiplicidad , uno de los valores propios deberá
tener multiplicidad 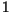 y el otro multiplicidad y el otro multiplicidad 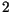 , si ponemos , si ponemos
 y y
 con con 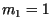 y y  entonces entonces
- Si ponemos
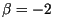 se obtiene se obtiene
- Si ponemos
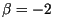 y si le aplicamos a y si le aplicamos a  las operaciones las operaciones
 y y
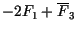 de manera consecutiva, obtenemos en cada aplicación, lo siguiente de manera consecutiva, obtenemos en cada aplicación, lo siguiente
Software:
Este artículo incluye dos programitas (applets)
en Java. El primero nos permite crear matrices con su respectiva
inversa y nos permite modificar 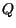 con
operaciones elementales. Para esto solo necesitamos indicar el valor de con
operaciones elementales. Para esto solo necesitamos indicar el valor de  ,
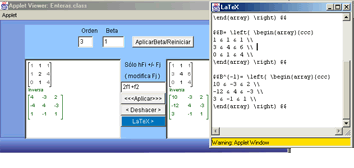
en el campo de texto respectivo. Este programita permite generar el texto LaTeX
de las 4 matrices. ,
en el campo de texto respectivo. Este programita permite generar el texto LaTeX
de las 4 matrices.
> Correr
el programa
> Descargar
el programa
El segundo es un programita para aplicar
operaciones elementales a una matriz con entradas enteras o fracciones (únicamente).

> Correr
el programa
> Descargar
el programa
Bibliografía:
- 1.
- Gilbert, R. "Companion Matrices with Integer Entries and
Integer Eigenvalues and Eigenvectors". American Mathematical
Monthly.
December, 1988.
- 2.
- Renaud, J. C. "Matrices with Integer Entries and
Integer Eigenvalues". American Mathematical Monthly.
March, 1983.
- 3.
- Noble, B. Daniel, J. "Algebra Lineal Aplicada".
Prentice-Hall, 1989.
|