Refrescamiento de imágenes
Como se puede comprobar en el "programita" que está más abajo, al arrastrar el triángulo se puede notar un "parpadeo". Esto se debe a que todos los pixeles de la imagen no se exhiben de manera simultánea.
Para evitar este problema, se exhibe primero una imagen mientras se construye la otra imagen 'fuera de pantalla' (es decir, no se despliega la imagen hasta que todos los cálculos hayan sido hechos), luego cuando llega el momento de exhibir la nueva imagen, se borra la imagen anterior desplegando un triángulo en blanco y luego se despliega la nueva imagen. Esta técnica se conoce como 'doble buffer' de gráficos. Esta fue la técnica que se uso en los "programitas" anteriores.
Alturas de un triángulo
Consideremos el problema de hacer un programa que despliega un triángulo (que se puede deformar arrastrando sus vértices) de tal manera que si arrastramos cualquiera de sus vértices, se despliega la altura correspondiente. Por ejemplo, arrastre cualquiera de los vértices del triángulo en el "programita" que sigue
Para implementar este programa necesitamos una manera eficiente para calcular el
punto en el lado opuesto al vértice, donde cae la altura. Sin duda una manera
natural es usar proyecciones. Si se conoce la orientación del triángulo también
se puede decidir rápidamente si hay que extender o no un lado y la dirección.
Consideremos una triágulo
ABC en la figura que sigue. Supongamos que queremos tirar la
altura desde el vértice en B hasta el lado opuesto.
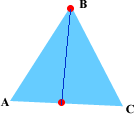
Si llamamos v = B - A y w = C - A
entonces la altura desde el vértice en B debe ser el segmento que va
desde el vértice en B hasta el punto
P=Proywv + A como se ve en
la figura que sigue
Puesto que Proywv = 
w
es claro que la altura cae en el segmento CA solo si
0 
1. Como w = C - A
entonces si
> 1, se debe extender el segmento AC a la derecha de C
y si
< 0 se debe extender a la izquierda de A.