- La instrucción While nos permite programar un ciclo. Mientras se cumpla la condición de prueba, se deben ejecutar las instrucciones contendidas en el ciclo. En el siguiente código, se muestra cómo imprimir los números del 1 al 5.
n = 1;
While[n <= 5,
Print[n];
n = n + 1;
]
- La instrucción Print nos permite escribir un mensaje combinando hileras y variables. En
el siguiente ejemplo se evidencia esta situación:
z = 5;
Print["El valor era de ", z]
- La instrucción If permite elegir entre dos situaciones excluyentes entre
sí. Mas formalmente, se pregunta por el valor de verdad de una proposición, si esta es verdadera, se ejecuta la primera instrucción asociada al If, en caso contrario la segunda. El siguiente código se encarga de imprimir un saludo.
If[3 < 5, Print["Hola"], Print[Adios]]
- La instrucción And nos permite preguntar por la conjunción de proposiciones lógicas. Como se sabe su valor de verdad será verdadero, toda vez que ambas proposiciones sean verdaderas y será falsa en cualquier otra combinación. El siguiente código escribe: Hola.
If[And[3 < 5, 5 < 10], Print["Hola"], Print[Adios]]
- La instrucción Random es clave en la GAE, se encarga de producir valores aleatorios. Si escribimos
Random[ ], Mathematica generará un valor real entre 0 y 1. Si escribimos, por ejemplo
Random[Integer, 1, 50], Mathematica generará un valor entero entre 1 y 50. La siguiente instrucción escribirá algunas veces,
Hola y otras, Adios.
If[Random[] < 0.5, Print["Hola"], Print[Adios]]
- Si tenemos una función como
f (x) = x2 + 3x - 2, una forma de implementarla en Mathematica es como sigue:
f[x_] = x^2 + 3x - 2. Observe que en esta última expresión escribimos x_ y no x. Además usamos paréntesis cuadrados, y no curvos.
- La función Round nos da el entero más cercano a un valor real
x. Así por ejemplo,
Round[1.7] devolvería el valor de 2, mientras que Round[-1.8],
-2.
- Mediante las funciones Numerator y Denominator podemos tomar el numerador y el denominador de una fracción. De esta forma si, por ejemplo
x = 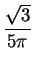 , entonces
, entonces Numerator[x] devolvería
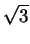 y
y Denominator[x],
5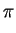 .
.
- Las funciones Max y Min proporcionan, en una lista de elementos, los valores máximos y mínimos respectivamente. De esta forma
Max[3, 5, -2, 4] devuelve 5 y Min[3, 5, -2, 4],
-2.
- La función Length calcula el número de elementos en una expresión dada. De esta forma si escribimos,
Length[{3, 5, -2, 4}], obtenemos un 4, si digitamos Length[3x^2 + 5x + 7], obtenemos un 3, si escribimos
Length[3x^2], obtenemos un 2.
- Las instrucciones Sum y Product nos permiten calcular sumatorias y productorias, respectivamente. En versiones más recientes de Mathematica, estas instrucciones han sido sustituidas con algunos iconos. Si deseamos, por ejemplo, calcular
debemos digitar
Sum[k^2, {k, 1, 5}] y Product[1/k, {k, 1, 5}].
- Podemos usar la expresión Expand para desarrollar una expresión algebraica. De esta forma, si escribimos
Expand[(a + b)^3], obtenemos
a3 + 3 a2 b + 3 a b2 + b3.
- Usamos la función Simplify para simplificar una expresión algebraica dada. Por lo tanto, si escribimos
Simplify[(x^2 - 4)/(x - 2)], obtenemos
x + 2.
- Podemos usar la instrucción Module para desarrollar funciones en las que el cálculo de la salida final necesita emplear variables locales.
Por ejemplo, si definimos la función
f[x_] := Module[{t}, t = (x + 2)^2; Expand[t]]
entonces la variable
t es tratada como local, de manera que si el valor de
t antes de invocar esta función era
2003, ese sigue siendo su valor después de invocar la función. Si digitamos f[t+1], obtenemos
t2 + 6 t + 9.
![]() , entonces
, entonces ![]() y
y ![]() .
.