Interpolación polinomial usando el Matlab
-
 barra
barra

-
 pag2
pag2
-
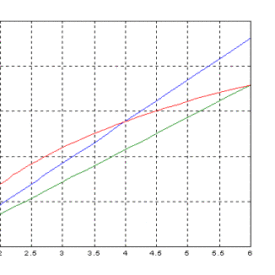 pag2.h1
pag2.h1
-
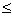 pag2.h10
pag2.h10
-
 pag2.h11
pag2.h11
-
 pag2.h12
pag2.h12
-
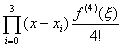 pag2.h13
pag2.h13
-
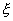 pag2.h14
pag2.h14
-
 pag2.h15
pag2.h15
-
 pag2.h16
pag2.h16
-
 pag2.h17
pag2.h17
-
 pag2.h18
pag2.h18
-
 pag2.h19
pag2.h19
-
 pag2.h2
pag2.h2
-
 pag2.h20
pag2.h20
-
 pag2.h21
pag2.h21
-
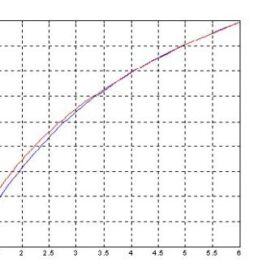 pag2.h3
pag2.h3
-
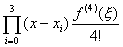 pag2.h4
pag2.h4
-
 pag2.h5
pag2.h5
-
 pag2.h6
pag2.h6
-
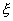 pag2.h7
pag2.h7
-
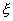 pag2.h8
pag2.h8
-
 pag2.h9
pag2.h9
-
 pag3
pag3
-
 pag4
pag4
-
 pag5
pag5
-
 pag5.h1
pag5.h1
-
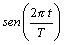 pag5.h2
pag5.h2
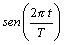
-
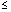 pag5.h3
pag5.h3
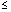
-
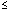 pag5.h4
pag5.h4
-
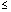 pag5.h5
pag5.h5
-
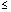 pag5.h6
pag5.h6
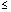
-
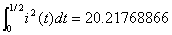 pag5.h7
pag5.h7
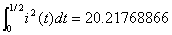
-
 pag5.h8
pag5.h8

-
 pag6
pag6
-
 wpe1
wpe1

-
 wpe2
wpe2
-
 wpe3
wpe3

-
 wpe5
wpe5
Tipo de documento
Autores
Lista de autores
Ascheri, María y Pizarro, Rubén A.
Resumen
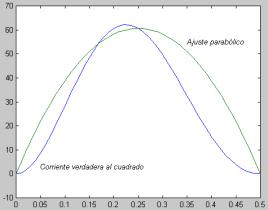
Con frecuencia se presenta la oportunidad de ajustar curvas a un conjunto de datos representados por puntos. Las técnicas desarrolladas para este fin dependen, fundamentalmente, de la naturaleza de los datos involucrados. El propósito de este trabajo es introducir a los alumnos de Cálculo Numérico, en el uso de la técnica de ajuste de curvas por medio de la interpolación en la solución de problemas de ingeniería, utilizando el paquete MATLAB. Además de que se espera que los alumnos asimilen y dominen los conceptos específicos impartidos referidos a la interpolación, se pretende que comprueben lo indispensable de la utilización de una computadora para resolver este tipo de problemas. También se espera, a partir de las distintas actividades propuestas a realizar por los alumnos, que observen y reconozcan cuándo la interpolación polinomial resulta apropiada arribando así, a resultados satisfactorios. Es decir que en esta primer instancia, se espera que los alumnos hayan aprendido a valorar la confiabilidad de las respuestas y ser capaces de escoger el mejor método (o métodos) para cualquier problema que deben afrontar frecuentemente en la práctica de la ingeniería o en diferentes problemas científicos o tecnológicos. Además, como resultado del análisis y comprensión de las actividades presentadas en este trabajo, se pretende introducir a los alumnos en el uso de la técnica de ajuste de curvas por medio de la regresión, a fin de que comprendan la diferencia entre interpolación y regresión, y que el confundirlos puede llevarlos a resultados erróneos.
Fecha
2001
Tipo de fecha
Estado publicación
Términos clave
Álgebra | Cálculo mental | Informáticos (recursos centro) | Números
Enfoque
Idioma
Revisado por pares
Formato del archivo
Referencias
[1] Chapra, S. - Canale, R. Métodos Numéricos para Ingenieros. Mc Graw-Hill. (1992). [2] García Merayo, F. - Nevot Luna, A. Análisis Numérico. Paraninfo. (1992). [3] Gordon, J. Algoritmos Numéricos. La Plata. (1985). [4] Kincaid, D. - Cheney, W. Análisis Numérico. Las Matemáticas del Cálculo Científico. Addison - Wesley Iberoamericana. (1994). [5] Mathew, J. - Kurtis, D. Métodos Numéricos con MATLAB. Prentice Hall. (2000).
