Para qué tantas hipótesis en el criterio de la integral
-
 cosx_x
cosx_x

-
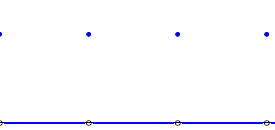 imagen1
imagen1

-
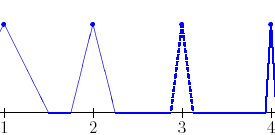 imagen2
imagen2
-
 img1
img1

-
 img10
img10
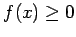
-
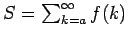 img100
img100
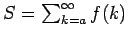
-
 img101
img101

-
 img102
img102

-
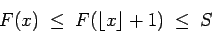 img103
img103
-
 img104
img104

-
 img105
img105

-
 img106
img106
-
 img107
img107
-
 img108
img108
-
 img109
img109
-
 img11
img11

-
 img110
img110
-
 img111
img111
-
 img112
img112

-
 img113
img113
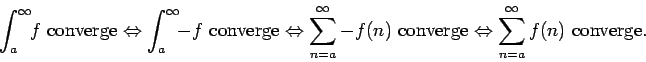
-
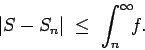 img114
img114
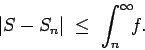
-
 img115
img115

-
 img116
img116
-
 img117
img117
-
 img118
img118
-
 img119
img119
-
 img12
img12
-
 img120
img120

-
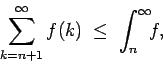 img121
img121
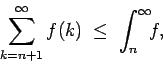
-
 img122
img122
-
 img123
img123

-
 img124
img124
-
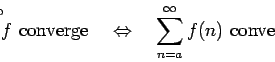 img125
img125

-
 img126
img126
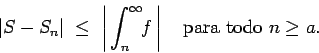
-
 img127
img127

-
 img128
img128
-
 img129
img129
-
 img13
img13
-
 img130
img130
-
 img131
img131
-
 img132
img132
-
 img133
img133
-
 img134
img134
-
 img135
img135
-
 img136
img136
-
 img137
img137

-
 img138
img138
-
 img139
img139
-
 img14
img14

-
 img140
img140
-
 img141
img141
-
 img142
img142
-
 img143
img143
-
 img144
img144

-
 img145
img145

-
 img146
img146
-
 img147
img147
-
 img148
img148
-
 img149
img149
-
 img15
img15

-
 img150
img150

-
 img151
img151
-
 img152
img152
-
 img153
img153
-
 img154
img154

-
 img155
img155
-
 img156
img156
-
 img157
img157
-
 img158
img158
-
 img159
img159
-
 img16
img16
-
 img160
img160
-
 img161
img161
-
 img162
img162
-
 img163
img163
-
 img164
img164
-
 img165
img165

-
 img166
img166
-
 img167
img167
-
 img168
img168
-
 img169
img169

-
 img17
img17
-
 img170
img170
-
 img171
img171
-
 img172
img172

-
 img173
img173
-
 img174
img174
-
 img175
img175

-
 img176
img176

-
 img177
img177
-
 img178
img178
-
 img179
img179

-
 img180
img180
-
 img181
img181

-
 img182
img182
-
 img183
img183

-
 img184
img184
-
 img185
img185

-
 img186
img186
-
 img19
img19
-
 img2
img2

-
 img20
img20

-
 img21
img21
-
 img22
img22
-
 img23
img23

-
 img24
img24

-
 img25
img25
-
 img26
img26
-
 img27
img27

-
 img28
img28
-
 img29
img29
-
 img3
img3

-
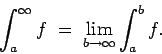 img30
img30
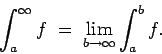
-
 img31
img31

-
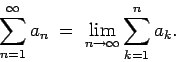 img32
img32
-
 img33
img33
-
 img34
img34
-
 img35
img35
-
 img36
img36

-
 img37
img37
-
 img38
img38
-
 img39
img39

-
 img4
img4

-
 img40
img40
-
 img41
img41
-
 img42
img42
-
 img43
img43

-
 img44
img44
-
 img45
img45
-
 img46
img46
-
 img47
img47

-
 img48
img48
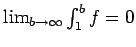
-
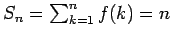 img49
img49
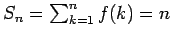
-
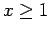 img5
img5
-
 img50
img50
-
 img51
img51
-
 img52
img52
-
 img53
img53

-
 img54
img54
-
 img55
img55
-
 img56
img56

-
 img57
img57
-
 img58
img58
-
 img59
img59
-
 img6
img6
-
 img60
img60
-
 img61
img61
-
 img62
img62
-
 img63
img63
-
 img64
img64
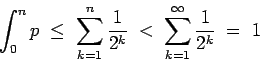
-
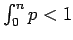 img65
img65
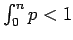
-
 img66
img66

-
 img67
img67

-
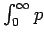 img68
img68
-
 img69
img69
-
 img7
img7

-
 img70
img70

-
 img71
img71
-
 img72
img72
-
 img73
img73
-
 img74
img74
-
 img75
img75

-
 img76
img76
-
 img77
img77

-
 img78
img78

-
 img79
img79
-
 img8
img8
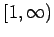
-
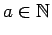 img80
img80
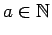
-
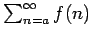 img81
img81
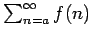
-
 img82
img82

-
 img83
img83

-
 img84
img84

-
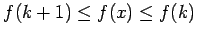 img85
img85
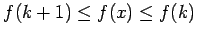
-
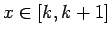 img86
img86
-
 img87
img87
-
 img88
img88
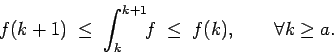
-
 img89
img89
-
 img9
img9
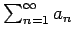
-
 img90
img90

-
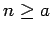 img91
img91
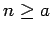
-
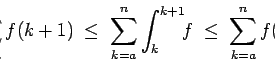 img92
img92

-
 img93
img93
-
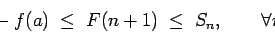 img94
img94
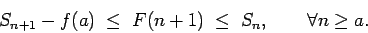
-
 img95
img95
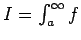
-
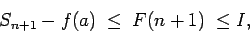 img96
img96
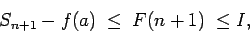
-
 img97
img97

-
 img98
img98

-
 img99
img99

-
 index
index
Tipo de documento
Autores
Lista de autores
Acuña, Luis
Resumen
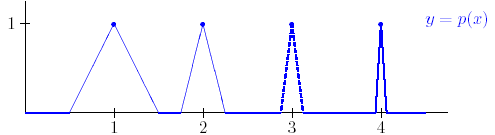
Se repasa el planteo tradicional del criterio de la integral para la convergencia de series (con las hipótesis de que la función en cuestión sea continua, positiva y decreciente, y la conclusión de que la serie y la integral impropia convergen ambas o divergen ambas). Se muestran ejemplos en los que fallan una o más de las hipótesis y la conclusión del criterio falla. Se demuestra que son innecesarias las hipótesis de continuidad y positividad, y finalmente que basta con una condición aún más débil que la de que la función sea decreciente. Los resultados se aplican tanto a la equivalencia entre la convergencia de la serie y la convergencia de la integral impropia como a la fórmula para la cota del error en las sumas parciales cuando la serie converge.
Fecha
2005
Tipo de fecha
Estado publicación
Términos clave
Enfoque
Nivel educativo
Educación superior, formación de pregrado, formación de grado | Educación técnica, educación vocacional, formación profesional
Idioma
Revisado por pares
Formato del archivo
Referencias
[1] Apostol, Tom; "Calculus''; 1986. [2] Apostol, Tom; "Análisis matemático''; 1977. [3] Bartle, Robert; "Introducción al análisis matemático de una variable''; 2003. [4] Lang, Serge; "Analysis I''; 1973. [5] Larson, Roland, Robert Hostetler y Bruce Edwards; "Cálculo''; 1998. [6] Rudin, Walter; "Principios de análisis matemático''; 1966. [7] Stewart, James; "Cálculo. Trascendentes tempranas''; 2001.
