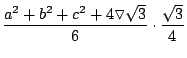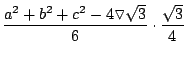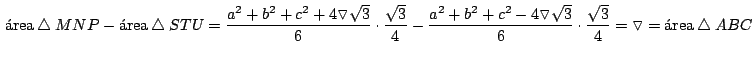Una vuelta de tuerca. O dos
Las propiedades vistas hasta el momento y en especial el teorema
de Napoleón, se siguen cumpliendo si
Si construimos los triángulos equiláteros
Aplicando el teorema del coseno en
de donde
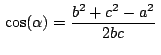
Siendo
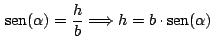
por lo que
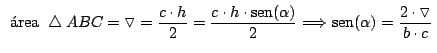
En
El teorema del coseno en
sustituyendo en
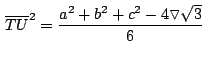
Procediendo de la misma forma podemos afirmar:
Aplicando el teorema del coseno en
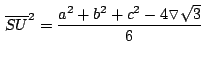
de forma similar podemos obtener:
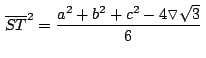
Sorpresa!
La diferencia de las áreas del triángulo de Napoleón exterior
Bajo la notación utilizada por lo visto en la tercera demostración
del teorema de Napoleón el cuadrado del lado del triángulo
De acuerdo a lo ya visto, el cuadrado del lado del triángulo de
Napoleón
Recordando que el área de un triángulo equilátero de lado
Si calculamos la diferencia de dichas áreas:
Cidse
- Revista
virtual Matemática, Educación e Internet -
ITCR
|




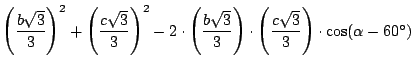
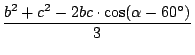
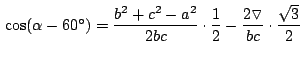
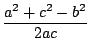
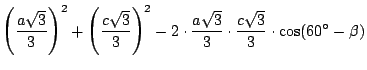
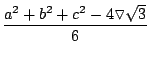

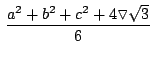 donde
donde
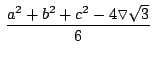 donde
donde
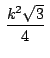 tenemos:
tenemos: