Una sucesión numérica es una función
a : IN 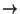 IR. Es común denotar an en vez de
a
IR. Es común denotar an en vez de
a n
n , y pensar en la sucesión como un ``conjunto
ordenado'' (o
, y pensar en la sucesión como un ``conjunto
ordenado'' (o 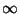 -étupla)
-étupla)
 a0
a0,
a1,
a2,...,
an,...
,
de ahí el nombre sucesión, pues cada número tiene sucesor, y
aparte de a0, todos tienen antecesor. A an se le llama el n -
ésimo término de la sucesión. La sucesión a se denota por
(an) o
 an
an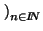 .
.
Ejemplo 2.6.1
Si
an = 1 para cada
n, tenemos
 an
an
=
1, 1,...

.
Ejemplo 2.6.2
Si
an =
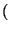
-1
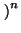
para cada
n, tenemos
 an
an
=
1, - 1, 1, - 1,...

.
Ejemplo 2.6.3
Para
an =

1 +
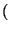
-1
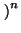

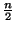
, para cada
n, entonces
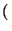 an
an
=
0, 0, 2, 0, 4,..., 0, 2
k, 0,...
.
De la misma forma se pueden considerar sucesiones definidas a partir de cierto
n. Así,
 an
an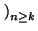 denotará la sucesión
a :
denotará la sucesión
a :  k, k + 1,...
k, k + 1,...
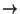 IR.
IR.
Ejemplo 2.6.4
Si
an =
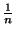
para
n 
1, se obtiene
 an
an
=
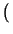
1,

,
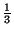
,...
.
Definición 2.6.1
La sucesión (
an) se llama creciente
si
a0 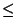 a1
a1 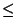 a2
a2 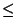
....
Nótese que esto es equivalente a tener
an  am
am, para
n  m
m.
Si la desigualdad es estricta, la sucesión se llama estrictamente
creciente. Similarmente, (
an) se llama decreciente
si
an  am
am para
n 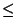 m
m.
Ejemplo 2.6.5
La sucesión
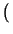
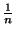
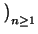
=
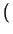
1,

,
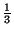
,...

es decreciente estrictamente.
Ejemplo 2.6.6
La sucesión constante
(
c)
n 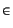 IN
IN =
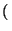 c
c,
c,
c,...

es creciente y decreciente.
Ejemplo 2.6.7
La sucesión
([
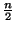
])
n 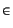 IN
IN =

0, 0, 1, 1, 2, 2,...
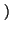
es creciente, pero no estrictamente creciente.
Ejemplo 2.6.8
La sucesión
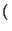
1, - 1, 1, - 1,...

= ((- 1)
n)
n 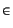 IN
IN no es creciente ni decreciente.
La sucesión
(an)n 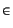 IN se llama acotada
superiormente, si existe
b
IN se llama acotada
superiormente, si existe
b  IR tal que
an
IR tal que
an 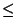 b,
b,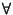 n
n  IN.
Equivalentemente,
IN.
Equivalentemente,
 an
an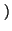 es acotada superiormente si su
rango
es acotada superiormente si su
rango
es un conjunto acotado superiormente. Similarmente,
 an
an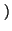 se llama acotada inferiormente
si su rango es acotado
inferiormente. La sucesión (an) se llama acotada
si es acotada superior e inferiormente (esto es,
si su rango es acotado). Nótese que
(an)n
se llama acotada inferiormente
si su rango es acotado
inferiormente. La sucesión (an) se llama acotada
si es acotada superior e inferiormente (esto es,
si su rango es acotado). Nótese que
(an)n 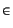 IN
es acotada si, y solo si, existe T > 0 tal que
| an|
IN
es acotada si, y solo si, existe T > 0 tal que
| an| 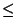 T,
T,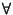 n
n  IN.
Es un buen ejercicio demostrar este hecho con detalle.
IN.
Es un buen ejercicio demostrar este hecho con detalle.
Ejemplo 2.6.9
Las sucesiones
(
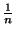
)
n  1
1,
((- 1)
n)
n  IN
IN y
(
c)
n 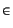 IN
IN son acotadas. En efecto, en los dos
primeros casos se puede tomar
T = 1, y en el tercer caso
T =
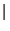 c
c
.
Ejemplo 2.6.10
La sucesión
([
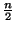
])
n 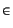 IN
IN es acotada inferiormente,
pero no superiormente. En efecto,

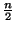
![$ \left.\vphantom{ \frac{n}{2}}\right]$](img169.gif)

0, pero
no existe
b tal que

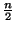
![$ \left.\vphantom{ \frac{n}{2}}\right]$](img169.gif)
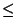 b
b para todo
n  IN
IN, pues si así lo fuera, 2
b + 2 sería cota superior de
IN.
Ejemplo 2.6.11
La sucesión
((- 1)
nn)
n 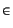 IN
IN no es acotada ni
superior ni inferiormente. Se invita al lector a verificar este hecho con todo detalle.
Subsections
![]() IR. Es común denotar an en vez de
a
IR. Es común denotar an en vez de
a![]() n
n![]() , y pensar en la sucesión como un ``conjunto
ordenado'' (o
, y pensar en la sucesión como un ``conjunto
ordenado'' (o ![]() -étupla)
-étupla)
![]() an
an![]() denotará la sucesión
a :
denotará la sucesión
a : ![]() k, k + 1,...
k, k + 1,...![]()
![]() IR.
IR.
![]() IN se llama acotada
superiormente, si existe
b
IN se llama acotada
superiormente, si existe
b ![]() IR tal que
an
IR tal que
an ![]() b,
b,![]() n
n ![]() IN.
Equivalentemente,
IN.
Equivalentemente,
![]() an
an![]() es acotada superiormente si su
rango
es acotada superiormente si su
rango