Para pasar a exponentes fraccionarios, tratemos de adivinar la
definición usando la propiedad 2. Si queremos que esta propiedad
siga siendo válida en IQ, debe tenerse
En otras palabras,
b : = a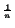 debe satisfacer bn = a. Esto nos
lleva a lo que ``por definición'' se llama ``raíz n-ésima'' de
a. Definimos entonces
debe satisfacer bn = a. Esto nos
lleva a lo que ``por definición'' se llama ``raíz n-ésima'' de
a. Definimos entonces
a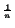
: =
![$\displaystyle \sqrt[n]{a}$](img276.gif)
.
Pero, ¿Quién nos dice que existe un número
real b tal que bn = a ?
La respuesta es: la completitud de IR. Para aclarar
esto bien, primero observemos que la función
f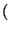 x
x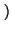 = xn
es estrictamente creciente en
= xn
es estrictamente creciente en
 0,
0,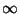
 . Esto puede
demostrarse por inducción:
. Esto puede
demostrarse por inducción:
También puede recurrirse a la identidad
xn -
yn =
 x
x -
y
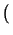 xn - 1
xn - 1 +
xn - 2 . y +
... +
x . yn - 2 +
yn - 1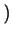
,
donde vemos que el segundo factor del lado derecho es positivo para x, y
positivos, y por lo tanto el signo de
xn - yn es el mismo que el de
x - y.
Ahora consideremos los conjuntos
A =
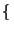 x
x 
0 :
xn <
a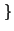
,
B =
 y
y 
0 :
yn  a
a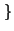
.
Note que
A 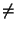
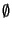 pues 0
pues 0  A, y
B
A, y
B 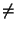
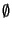 pues a + 1
pues a + 1  B.
Además, para x
B.
Además, para x  A y y
A y y  B se tiene x
B se tiene x 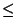 y. El axioma del extremo
superior asegura la existencia de
y. El axioma del extremo
superior asegura la existencia de
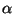
 B tal que
x
B tal que
x 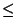
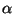
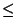 y,
para todo x
y,
para todo x  A y todo y
A y todo y  B. Luego se demuestra que
B. Luego se demuestra que
 = a, y
por lo tanto
= a, y
por lo tanto 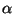 es la raíz n -ésima de a, y se denota por
es la raíz n -ésima de a, y se denota por
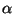 =
= ![$ \sqrt[n]{a}$](img126.gif) . En el capítulo 1 se demostró el caso n = 2. El
caso general se demuestra, usando sucesiones, en el ejercicio 37 del
capítulo 1.
. En el capítulo 1 se demostró el caso n = 2. El
caso general se demuestra, usando sucesiones, en el ejercicio 37 del
capítulo 1.
Una vez resuelto el problema de la existencia de las raíces,
usando la propiedad 2 como modelo vemos que para
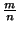
 IQ
debe definirse
IQ
debe definirse
Nota: Tomando
b = ![$ \sqrt[n]{a}$](img126.gif) tenemos bn = a, y por la propiedad 2
(con exponente natural) se sigue que
lo que significa que bm es la raíz n -ésima de am. Esto
demuestra que
o equivalentemente:
tenemos bn = a, y por la propiedad 2
(con exponente natural) se sigue que
lo que significa que bm es la raíz n -ésima de am. Esto
demuestra que
o equivalentemente:
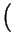 a1/n
a1/n
=
am/n.
El próximo paso es verificar las propiedades 1,...,5 para
exponentes racionales. Esto es, para a, b > 0 se tiene:
-
ar . as = ar + s,
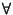 r, s
r, s  IQ
IQ
-
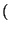 ar
ar = ar . s,
= ar . s,
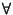 r, s
r, s  IQ
IQ
-
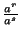 = ar - s,
= ar - s,
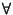 r, s
r, s  IQ
IQ
-
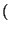 ab
ab = ar . br,
= ar . br, 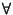 r
r  IQ
IQ
-
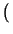
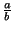
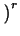 =
= 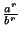 ,
, 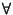 r
r  IQ.
IQ.
Mostremos como ejemplo la propiedad 2: Si
r = 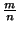 y
s =
y
s = 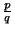 , con n > 0 y q > 0, tenemos que
, con n > 0 y q > 0, tenemos que
El único paso que no está aún justificado es la igualdad
![$ \sqrt[q]{\sqrt[n]{a^{mp}}}$](img514.gif) =
= ![$ \sqrt[qn]{a^{mp}}$](img515.gif) . Para demostrar esto sean
b = amp y
c =
. Para demostrar esto sean
b = amp y
c = ![$ \sqrt[q]{\sqrt[n]{b}}$](img517.gif) . Entonces
cq =
. Entonces
cq = ![$ \sqrt[n]{b}$](img518.gif) , y por lo
tanto
, y por lo
tanto
 cq
cq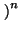 = b. Por la propiedad 2 para exponentes
enteros tenemos que cqn = b, y esto significa que
c =
= b. Por la propiedad 2 para exponentes
enteros tenemos que cqn = b, y esto significa que
c = ![$ \sqrt[qn]{b}$](img521.gif) =
= ![$ \sqrt[qn]{a^{mp}}$](img515.gif) .
.
Ejemplo 3.3.1
Resolver la ecuación
x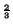
- 3
x
+ 2 = 0. Tomando
t =
x
tenemos
t2 - 3
t + 2 = 0, y resolviendo se obtiene
t 
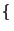
1, 2
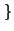
. Luego, la solución es
x 

1, 8
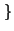
.
Ejemplo 3.3.2
Resolver
4x - 2x + 1 + 1 = 0. Tomando t = 2x tenemos
4x = 22x = t2,
2x + 1 = 2 . 2x = 2t, así que la ecuación es
t2 - 2t + 1 = 0, y
entonces t = 1. Luego la solución es x = 0.
Concluimos este capítulo demostrando que la función
f : IQ 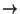 IR, definida por
f
IR, definida por
f r
r = ar, es
estrictamente creciente en IQ, para a > 1. Esto es
= ar, es
estrictamente creciente en IQ, para a > 1. Esto es
ar <
as si
r <
s, con
r,
s 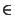 IQ
IQ.
En efecto, para
n  IN y b > 0 tenemos
IN y b > 0 tenemos
bn > 1 si y solo si b > 1,
por ser
f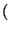 x
x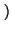 = xn estrictamente creciente. Luego, si
s - r =
= xn estrictamente creciente. Luego, si
s - r = 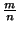 > 0, podemos asumir que
m, n
> 0, podemos asumir que
m, n  IN, así que
am > 1. Ahora, como
b = as - r = am/n satisface
bn = am > 1,
concluimos que b > 1. Finalmente
IN, así que
am > 1. Ahora, como
b = as - r = am/n satisface
bn = am > 1,
concluimos que b > 1. Finalmente
as = aras - r = arb > ar, si r < s.
![]() x
x![]() = xn
es estrictamente creciente en
= xn
es estrictamente creciente en
![]() 0,
0,![]()
![]() . Esto puede
demostrarse por inducción:
. Esto puede
demostrarse por inducción:
![]()
![]() IQ
debe definirse
IQ
debe definirse
![]() y
s =
y
s = ![]() , con n > 0 y q > 0, tenemos que
, con n > 0 y q > 0, tenemos que
![]() ar
ar![]()
![]()
![]()
![]() =
= ![]()
![]() =
= ![]()
![]() = ars.
= ars.![]() =
= ![]() . Para demostrar esto sean
b = amp y
c =
. Para demostrar esto sean
b = amp y
c = ![]() . Entonces
cq =
. Entonces
cq = ![]() , y por lo
tanto
, y por lo
tanto
![]() cq
cq![]() = b. Por la propiedad 2 para exponentes
enteros tenemos que cqn = b, y esto significa que
c =
= b. Por la propiedad 2 para exponentes
enteros tenemos que cqn = b, y esto significa que
c = ![]() =
= ![]() .
.
![]() IR, definida por
f
IR, definida por
f![]() r
r![]() = ar, es
estrictamente creciente en IQ, para a > 1. Esto es
= ar, es
estrictamente creciente en IQ, para a > 1. Esto es