Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28 

La función logarítmica

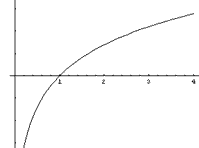
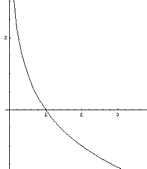
Dado que la función exponencial de base a es biyectiva de IR en $\left]\vphantom{ 0,\infty}\right.$0,$\infty$$\left.\vphantom{ 0,\infty}\right[$, existe su inversa, que denotamos

log_a : $$\left]\vphantom{ 0,\infty}\right.$$0,$$\infty$$$$\left.\vphantom{ 0,\infty}\right[$$ $$\rightarrow$$ IR.

Tenemos entonces, por definición de función inversa, que

a^x = y $$\Leftrightarrow$$ x = log_ay.

Escrito de otra forma:

log_aa^x = x,$$\forall$$x $$\in$$ IR;  a^log_ay = y,$$\forall$$y > 0.

El gráfico de la función log_a se obtiene del gráfico de f (x) = a^x, reflejando con respecto a la recta y = x. En el caso a > 1 obtenemos,

y si 0 < a < 1 se obtiene

Basados en las propiedades de la función exponencial, podemos deducir las propiedades de la función logarítmica. Veamos:

• log_a1 = 0, pues a⁰ = 1.

• log_aa = 1, pues a¹ = a.

• Sean t = log_ax, s = log_ay. Entonces a^t = x, a^s = y. Luego x ^. y = a^{t .} a^s = a^{t + s}, de donde t + s = log_a$\left(\vphantom{ x\cdot y}\right.$x ^. y$\left.\vphantom{ x\cdot y}\right)$. Esto demuestra que
  log_a$$\left(\vphantom{ x\cdot y}\right.$$x ^. y$$\left.\vphantom{ x\cdot y}\right)$$ = log_ax + log_ay,  $$\forall$$x, y > 0.

• Sea t = log_ax. Entonces a^ts = $\left(\vphantom{ a^{t}}\right.$a^t$\left.\vphantom{ a^{t}}\right)^{s}_{}$ = x^s, $\forall$s $\in$ IR, de donde ts = log_ax^s. Esto demuestra que
  log_ax^s = s log_ax,  $$\forall$$x > 0,  $$\forall$$s $$\in$$ IR.

  En particular con s = - 1 obtenemos

  log_a$${\frac{1}{x}}$$ = - log_ax,  $$\forall$$x > 0.

• Combinando las dos propiedades anteriores obtenemos
  log_a$${\frac{x}{y}}$$ = log_ax - log_ay,$$\forall$$x, y > 0.

• La función log_ax es estrictamente creciente en $\left]\vphantom{ 0,\infty}\right.$0,$\infty$$\left.\vphantom{ 0,\infty}\right[$, si a > 1, por ser la inversa de una función creciente.

  En efecto, sea 0 < x < y, y sea t = log_ax, s = log_ay. Supongamos que t $\geq$ s. Entonces, como la exponencial de base a es creciente tendríamos x = a^t $\geq$ a^s = y, lo cual es imposible. Entonces log_ax = t < s = log_ay.

• Cambio de base:

  Sean a, b > 0, a $\neq$ 1,  b $\neq$ 1. Sean x > 0, t = log_ax, s = log_bx. Tenemos a^t = x = b^s, de donde t = log_ab^s = s log_ab. Luego

  s = $${\frac{t}{\log_{a}b}}$$,

   

  lo que demuestra que
  log_bx = $${\frac{\log_{a}x}{\log_{a}b}}$$.

   Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28