|
|
| Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
1 + ![]() + ... +
+ ... + ![]() = 2 -
= 2 - ![]() ,
n
,
n ![]() IN.
IN.
1 + r + ... + rn = ![]() ,
n
,
n ![]() IN, r
IN, r ![]() 1.
1.
Tal ![]() se llama el extremo inferior de B, y se denota
se llama el extremo inferior de B, y se denota
![]() = inf B.
Sug. El conjunto
= inf B.
Sug. El conjunto
| an = |
an = cosn |
an = n(- 1)n |
| an = 1 + (- 1)n | an =  |
an = |
an = 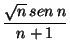 |
an = 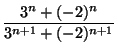 |
an = 1 + |
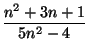 , cn =
, cn =
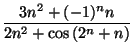 , cn =
, cn =
 .
.
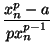 ,
, 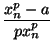
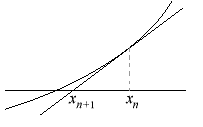
Nota: Esta sucesión se obtiene aplicando el método de
Newton a la función
f (x) = xn - a. Es decir, para cada n se considera
la recta tangente al gráfico de f, en el punto
![]() xn, f
xn, f![]() xn
xn![]()
![]() , y se define xn + 1 como el punto en que esa recta
corta al eje x. En efecto, la recta tangente en el punto
, y se define xn + 1 como el punto en que esa recta
corta al eje x. En efecto, la recta tangente en el punto
![]() xn, f
xn, f![]() xn
xn![]()
![]() tiene ecuación
tiene ecuación
 = xn -
= xn - 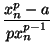 = xn + 1.
= xn + 1.
Usted debe demostrar que
![]() xn
xn![]() converge a la raíz
positiva de f, lo cual es geométricamente evidente.
converge a la raíz
positiva de f, lo cual es geométricamente evidente.