Desde temprana edad hemos aprendido que todo
número real x tiene expansión decimal
c0, c1c2..., y
que esto significa, en el caso que x sea positivo,
x =
c0 +
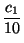
+
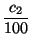
+....
Los dígitos
c1, c2,... son números naturales entre 0 y
9, mientras que c0 es un número entero. Por ejemplo,
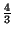
= 1, 333...,

= - 3, 500...,
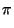
= 3, 141 592 653 589 793....
Consideremos primero un número real
x  [0, 1[. Vamos a demostrar
que efectivamente existe una sucesión de naturales
[0, 1[. Vamos a demostrar
que efectivamente existe una sucesión de naturales
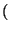 cn
cn , con
cn
, con
cn 
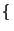 0, 1,..., 9
0, 1,..., 9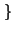 , tales que
, tales que
En tal caso decimos que x tiene expansión decimal
0, c1c2c3....
Para empezar, debemos tener
o lo que es lo mismo,
c1 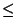 10x < c1 + 1. Debemos definir entonces
c1 : =
10x < c1 + 1. Debemos definir entonces
c1 : = 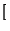 10x
10x![$ \left.\vphantom{ 10x}\right]$](img311.gif) (la parte entera de 10x). Nótese que esta
es la única opción. Luego, habiendo definido
c1, c2,..., cn - 1, debemos definir cn tal que
Esto es equivalente a
lo que significa
(la parte entera de 10x). Nótese que esta
es la única opción. Luego, habiendo definido
c1, c2,..., cn - 1, debemos definir cn tal que
Esto es equivalente a
lo que significa
cn 
10
nx -
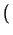
10
n - 1c1 + 10
n - 2c2 +...+ 10
cn - 1
<
cn + 1.
La única posibilidad es definir
cn : =

10
nx -
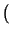 c1
c110
n - 1 +
c210
n - 2 +...+
cn - 110
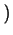
![$\displaystyle \left.\vphantom{ 10^{n}x-\left( c_{1}10^{n-1}+c_{2}10^{n-2}+\ldots
+c_{n-1}10\right) }\right]$](img321.gif)
.
Esto define la sucesión
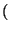 cn
cn por recurrencia, de tal
forma que
rn =
por recurrencia, de tal
forma que
rn =  +
+ 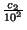 +...+
+...+  satisface
satisface
rn  x
x <
rn +
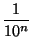
.
Consecuentemente
 rn - x
rn - x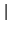 <
< 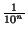
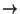 0,
así que
rn
0,
así que
rn 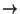 x. Claramente, la sucesión
x. Claramente, la sucesión
 rn
rn es creciente, pues
Además
es creciente, pues
Además
rn + 1 +  |
= rn + 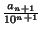 + +  |
| |
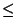 rn + rn + 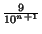 + +  |
| |
= rn + 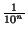 . . |
Esto demuestra que la sucesión
sn = rn + 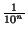 es
decreciente, y además
sn
es
decreciente, y además
sn 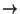 x. A continuación resumimos
este resultado:
x. A continuación resumimos
este resultado:
Teorema 6
Dado un número real
x, existe una única sucesión de naturales
cn 
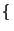
0, 1,..., 9
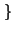
tales que
Además, la sucesión
 rn
rn
definida arriba es
creciente y converge a
x, mientras que la sucesión
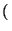 sn
sn
definida por
sn =
rn +
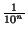
es decreciente y
converge a
x.
Definición 2.7.1
Si
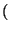 cn
cn
es la sucesión del teorema anterior, se dice
que
x tiene expansión decimal
0,
c1c2..., y se escribe
x = 0,
c1c2....
En general, si x > 0 definimos
c0 : = 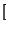 x
x![$ \left.\vphantom{ x}\right]$](img71.gif) , obteniendo
x - c0
, obteniendo
x - c0  [0, 1[. Si la expansión decimal de x - c0 es
0, c1c2..., escribimos
x = c0, c1c2....
[0, 1[. Si la expansión decimal de x - c0 es
0, c1c2..., escribimos
x = c0, c1c2....
Ejemplo 2.7.1
Dado
x =
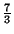
, tenemos
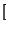 x
x![$ \left.\vphantom{ x}\right]$](img71.gif)
= 2, y
x - 2 =
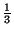
= 0, 333.... Entonces
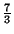
= 2, 333....
Finalmente, para hallar la expansión de un número negativo x, se
halla primero la expansión de
 x
x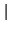 , y luego simplemente se
le coloca el signo ``-''.
, y luego simplemente se
le coloca el signo ``-''.
Ejemplo 2.7.2
Para
x = -

tenemos
 x
x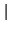
=

= 1 +

, y

= 0, 6. Luego
x = - 1, 6.
Nota: Uno se puede preguntar si dada una sucesión cualquiera
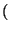 cn
cn , con
cn
, con
cn 
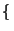 0,..., 9
0,..., 9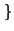 , siempre
existe un x cuya expansión decimal sea
0, a1a2.... La
respuesta es ``casi sí''. Para aclarar esto, tomemos por ejemplo cn = 9 para todo n. En tal caso
rn = 0, 99...9, donde aparecen n nueves,
mientras que
rn +
, siempre
existe un x cuya expansión decimal sea
0, a1a2.... La
respuesta es ``casi sí''. Para aclarar esto, tomemos por ejemplo cn = 9 para todo n. En tal caso
rn = 0, 99...9, donde aparecen n nueves,
mientras que
rn + 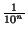 = 1. Nótese que no existe
x
= 1. Nótese que no existe
x  IR tal que
IR tal que
Entonces la expansión decimal
0, no representaría
ningún número real. Para corregir esto debemos admitir la posibilidad
x = rn +
no representaría
ningún número real. Para corregir esto debemos admitir la posibilidad
x = rn + 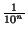 , con lo que obtendríamos en particular
0,
, con lo que obtendríamos en particular
0, = 1. Nótese que sin embargo esto implica que no hay
unicidad de la representación decimal en ciertos casos. Por ejemplo:
= 1. Nótese que sin embargo esto implica que no hay
unicidad de la representación decimal en ciertos casos. Por ejemplo:
1 = 1, 000...= 0, 999...,

= 0, 500...= 0, 499....
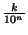 , para algún
k
, para algún
k  IZ y algún
n
IZ y algún
n  IN.
IN.
![]() [0, 1[. Vamos a demostrar
que efectivamente existe una sucesión de naturales
[0, 1[. Vamos a demostrar
que efectivamente existe una sucesión de naturales
![]() cn
cn![]() , con
cn
, con
cn ![]()
![]() 0, 1,..., 9
0, 1,..., 9![]() , tales que
, tales que
![]()
![]() +
+ ![]()
![]() rn +
rn + ![]() +
+ ![]()
![]() .
.![]() es
decreciente, y además
sn
es
decreciente, y además
sn ![]() x. A continuación resumimos
este resultado:
x. A continuación resumimos
este resultado:
![]() x
x![]() , obteniendo
x - c0
, obteniendo
x - c0 ![]() [0, 1[. Si la expansión decimal de x - c0 es
0, c1c2..., escribimos
x = c0, c1c2....
[0, 1[. Si la expansión decimal de x - c0 es
0, c1c2..., escribimos
x = c0, c1c2....
![]() x
x![]() , y luego simplemente se
le coloca el signo ``-''.
, y luego simplemente se
le coloca el signo ``-''.
![]() cn
cn![]() , con
cn
, con
cn ![]()
![]() 0,..., 9
0,..., 9![]() , siempre
existe un x cuya expansión decimal sea
0, a1a2.... La
respuesta es ``casi sí''. Para aclarar esto, tomemos por ejemplo cn = 9 para todo n. En tal caso
rn = 0, 99...9, donde aparecen n nueves,
mientras que
rn +
, siempre
existe un x cuya expansión decimal sea
0, a1a2.... La
respuesta es ``casi sí''. Para aclarar esto, tomemos por ejemplo cn = 9 para todo n. En tal caso
rn = 0, 99...9, donde aparecen n nueves,
mientras que
rn + ![]() = 1. Nótese que no existe
x
= 1. Nótese que no existe
x ![]() IR tal que
IR tal que