El lector probablememente sabe muy bien que
dado a > 0, 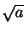 es un número real positivo tal que
es un número real positivo tal que

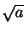
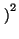 = a. En esta sección usamos la completitud de
IR para darle rigor a esta definición. En otras palabras,
demostraremos que la función
f : IR+
= a. En esta sección usamos la completitud de
IR para darle rigor a esta definición. En otras palabras,
demostraremos que la función
f : IR+  IR+,
definida por
f (x) = x2, es sobreyectiva. Primero, y para enfatizar la
diferencia entre IQ y IR, vamos a demostrar que esto no es
posible hacerlo en IQ. Específicamente, vamos a demostrar que:
IR+,
definida por
f (x) = x2, es sobreyectiva. Primero, y para enfatizar la
diferencia entre IQ y IR, vamos a demostrar que esto no es
posible hacerlo en IQ. Específicamente, vamos a demostrar que:
Lema 2.5.1
No existe
r  IQ
IQ tal que
r2 = 2.
Prueba:
En efecto, supongamos que sí existe tal r. Entonces se puede
escribir
r =
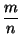
,
donde m, n son naturales, y al menos uno de ellos es impar. Se sigue entonces
que
m2 = 2n2, y consecuentemente m2 es par, lo que implica que m
también es par (¿por qué?), esto es m = 2k para
algún
k  IZ. Luego
IZ. Luego
2n2 = m2 = 4k2,
y obtenemos que n2 también es par, con lo cual n es par. Como esto
es contradictorio, no existe tal r.
Este hecho, junto con el lema siguiente, permite concluir que existe
un número real
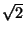
 II.
II.
Lema 2.5.2
Dado
a > 0, existe un número
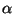
> 0 tal que
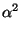
=
a. A tal
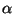
se le llama la raíz cuadrada de
a, y se le denota
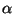
=
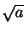
.
Prueba:
Defina los conjuntos
A =
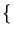 x
x 
0 :
x2 <
a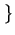
,
B =
 y
y > 0 :
y2 >
a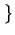
.
Como a > 0 tenemos que 0  A, así que
A
A, así que
A 
 . Además,
como
(a + 1)2 > a + 1 > a, tenemos
B
. Además,
como
(a + 1)2 > a + 1 > a, tenemos
B 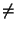
 . La igualdad
demuestra que para x, y > 0 se tiene
. La igualdad
demuestra que para x, y > 0 se tiene
x >
y  x2
x2 >
y2.
Luego, dados x  A y y
A y y  B se tiene
x2 < a < y2, con lo que x < y.
Por la completitud de IR existe
B se tiene
x2 < a < y2, con lo que x < y.
Por la completitud de IR existe
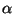
 IR tal que
x
IR tal que
x 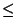
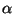
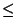 y para todo x
y para todo x  A y todo y
A y todo y  B. Para demostrar que
B. Para demostrar que
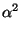 = a, debemos descartar las posibilidades
= a, debemos descartar las posibilidades
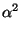 > a y
> a y
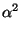 < a. Veamos:
< a. Veamos:
- 1.
- Si
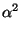 < a, tome
0 <
< a, tome
0 < 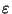 < 1. Note que
< 1. Note que
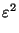 <
< 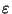 , y entonces
, y entonces
(

+
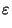
)
2 =
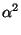
+ 2

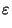
+
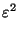
<
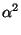
+ (2

+ 1)
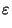
.
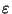 <
< 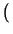 a -
a - 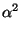
 /
/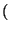 2
2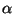 + 1
+ 1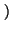 , se sigue que
, se sigue que
(

+
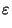
)
2 <
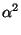
+ (2

+ 1)
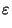
<
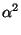
+
 a
a -
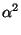
=
a.
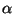 +
+ 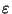
 A, contradiciendo el hecho que
A, contradiciendo el hecho que 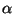 es
cota superior de A.
es
cota superior de A.
- 2.
- Si
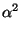 > a, note que
Si
0 <
> a, note que
Si
0 < 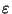 <
< 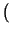
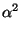 - a
- a /2
/2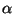 , obtenemos
Pero entonces
, obtenemos
Pero entonces
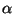 -
- 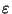
 B, lo que contradice el hecho que
B, lo que contradice el hecho que
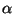 es cota inferior del conjunto B.
es cota inferior del conjunto B.
Un argumento similar al anterior se usa para demostrar que dados
a > 0,
n  IN, existe
IN, existe 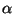 > 0 tal que
> 0 tal que
 = a. Tal
= a. Tal
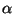 se llama la raíz n - ésima de a, y se denota
se llama la raíz n - ésima de a, y se denota
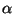 =
= ![$ \sqrt[n]{a}$](img126.gif) .
.
Inicio
1
2
3
4
5
6
7
8 9 10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
![]() es un número real positivo tal que
es un número real positivo tal que
![]()
![]()
![]() = a. En esta sección usamos la completitud de
IR para darle rigor a esta definición. En otras palabras,
demostraremos que la función
f : IR+
= a. En esta sección usamos la completitud de
IR para darle rigor a esta definición. En otras palabras,
demostraremos que la función
f : IR+ ![]() IR+,
definida por
f (x) = x2, es sobreyectiva. Primero, y para enfatizar la
diferencia entre IQ y IR, vamos a demostrar que esto no es
posible hacerlo en IQ. Específicamente, vamos a demostrar que:
IR+,
definida por
f (x) = x2, es sobreyectiva. Primero, y para enfatizar la
diferencia entre IQ y IR, vamos a demostrar que esto no es
posible hacerlo en IQ. Específicamente, vamos a demostrar que:
![]()
![]() II.
II.
![]() IN, existe
IN, existe ![]() > 0 tal que
> 0 tal que
![]() = a. Tal
= a. Tal
![]() se llama la raíz n - ésima de a, y se denota
se llama la raíz n - ésima de a, y se denota
![]() =
= ![]() .
.