|
|
| Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
log28, log93, log2![]() , log10(0.0001).
, log10(0.0001).
![$\displaystyle \begin{array}[c]{ccccc}%%
\left( \sqrt{2}\right) ^{x^{2}}=2 & 3^{...
...n2}=2^{\ln x} & \frac
{3^{x}-2^{x}}{2^{x}-1}=-1 & x^{2}=2^{\ln x} &
\end{array}$](img726.gif)
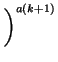 .
.
Luego considere la sucesión (Sn) definida por
Sn = ![]()
![]() , con a > 0 fijo. Muestre que (Sn) es
creciente y acotada superiormente, y concluya que (Sn) converge a cierto
límite
S
, con a > 0 fijo. Muestre que (Sn) es
creciente y acotada superiormente, y concluya que (Sn) converge a cierto
límite
S ![]() ea. Usando la fórmula del binomio otra vez se tiene
ea. Usando la fórmula del binomio otra vez se tiene
| f (x) | = ln |
| j(x) | = |
![$\displaystyle \begin{array}[c]{llll}%%
{\displaystyle\int}
xe^{x^{2}}dx\; &
{\d...
...frac{e^{x}dx}{e^{x}+1}\; &
{\displaystyle\int}
\frac{dx}{e^{x}+1}%%
\end{array}$](img853.gif)
 , sinh x =
, sinh x =  ,
,
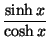 , coth x =
, coth x =


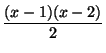
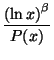 = 0,
= 0,
| Sm | < Sn = Sm + |
| < Sm + |
Inicio 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28