Definiciones por recurrencia
Muchas veces, para definir una función
f : IN 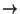 A, se
hace uso implícito del principio de inducción. Por ejemplo, cuando se
define
A, se
hace uso implícito del principio de inducción. Por ejemplo, cuando se
define
an = a . a . ... . a (n veces),
realmente se está pensando en la definición: a0 = 1,
an + 1 = an . a. Esto define a0, y asumiendo que an está
definido, permite definir an + 1. El principio de inducción garantiza
que esta es una buena definición de la función
f :
IN 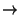 IR
IR,
f (
n) =
an.
En lo que sigue hacemos uso de este principio.
Ejemplo 2.3.8 (El factorial)
Se define 0! = 1, y para
n  IN
IN,
(
n + 1)! = (
n + 1)
. n!. Tenemos entonces
1! = 1
. 0! = 1,
2! = 2
. 1! = 2
. 1,
3! = 3
. 2
. 1, y en general
n! =
n . (
n - 1)
... 3
. 2
. 1.
Ejemplo 2.3.9
Dada una función
f :
IN 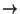 IR
IR, podemos definir la
suma
Sn = f (0) +...+ f (n)
inductivamente así:
S0 = f (0), Sn + 1 = Sn + f (n + 1).
A veces se usa la notación
ak =
f (
k), obteniendo
Sn = a0 +...+ an,
que también se denota por
Sn =
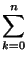 ak
ak.
Note que por definición se tiene
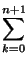 ak
ak =
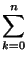 ak
ak +
an + 1.
Si se comienza en 1, se denota
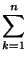 ak
ak =
a1 +...+
an.
Ejemplo 2.3.10
Un caso particular del ejemplo anterior es la suma
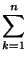 k
k =
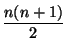
,
que estudiamos anteriormente.
Ejemplo 2.3.11
Demostrar que
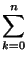 k . k
k . k! = (
n + 1)! - 1,
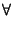 n
n 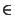 IN
IN.
Para
n = 0 la suma del lado izquierdo es
0
. 0! = 0, mientras que al lado
derecho tenemos
(0 + 1)! - 1 = 0. Entonces la igualdad es válida para
n = 0.
Supongamos que la igualdad es válida para n, y probémosla para
n + 1. Tenemos
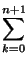 k . k
k . k! =
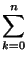 k . k
k . k! + (
n + 1)
. (
n + 1)!,
y por hipótesis de inducción se sigue que
 k . k! k . k! |
= (n + 1)! - 1 + (n + 1) . (n + 1)! |
| |
= (1 + n + 1)(n + 1)! - 1 |
| |
= (n + 2)(n + 1)! - 1 |
| |
= (n + 2)! - 1. |
Esto demuestra la igualdad para n + 1, y por el principio de inducción se
sigue que es válida para todo
n  IN.
IN.
Ejemplo 2.3.12
Demostrar que 2
n <
n!, para todo
n 
4.
Para n = 4 tenemos
24 = 16 < 24 = 4!. Ahora supongamos que 2n < n! para
algún n  4. Entonces
4. Entonces
2n + 1 = 2 . 2n < 2 . n! < (n + 1) . n! = (n + 1)!,
con lo que
n + 1 también satisface la desigualdad. El principio de
inducción se encarga del resto.
![]() A, se
hace uso implícito del principio de inducción. Por ejemplo, cuando se
define
A, se
hace uso implícito del principio de inducción. Por ejemplo, cuando se
define
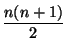 ,
,
![]() IN.
IN.![]() 4. Entonces
4. Entonces