Las identidades de la sección anterior nos dan una idea de lo
que debemos hacer en el caso de exponentes enteros. Si, por ejemplo, queremos
que la tercera identidad sea válida con n = m, debemos tener
a0 =
an - n =

= 1.
Debemos definir entonces a0 : = 1. Nótese que no hemos
demostrado que a0 = 1, solo hemos justificado por qué definirlo
así.
Tratemos ahora de definir a-m, para
m  IN. Para comenzar, si
queremos que la propiedad 1 sea válida con exponentes negativos, debemos
tener por ejemplo
IN. Para comenzar, si
queremos que la propiedad 1 sea válida con exponentes negativos, debemos
tener por ejemplo
a-2 . a2 = a-2 + 2 = a0 = 1,
y dividiendo por a2 obtenemos
a-2 =
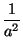
.
En general, tomando m en lugar de 2 obtenemos que para que se cumpla
a-m . am = a0, debe definirse:
Con esto tenemos definido az, para a 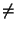 0 y cualquier
z
0 y cualquier
z  IZ.
IZ.
En este punto debemos demostrar que las propiedades 1,...,5
siguen siendo válidas para todo
n, m  IZ. Por ejemplo,
nótese que
IZ. Por ejemplo,
nótese que
a-4 . a3 =
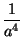 . a3
. a3 =
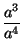
=



=
a-1 =
a-4 + 3.
El caso general no es más complicado que esto. Tomando por ejemplo p  m tenemos
m tenemos
a-p . am =
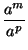
=



=
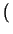 ap - m
ap - m
=
a-  p - m
p - m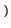
=
a-p + m.
Esto demuestra la propiedad 1 en el caso n = - p, con p  m. El caso p < m
es más fácil.
m. El caso p < m
es más fácil.
Similarmente procedemos con la propiedad 2: Si n = - p < 0 y m > 0,
tenemos
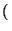 an
an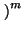
=
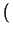 a-p
a-p
=
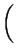

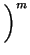
=
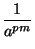
=
a-pm =
anm,
donde usamos las propiedades 2 y 5 para
p, m  IN. Los otros casos se
tratan de manera similar.
IN. Los otros casos se
tratan de manera similar.
Ejemplo 3.2.1
Simplificar la expresión
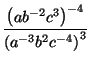
.
Aplicando las propiedades 2 y 5 para exponentes enteros tenemos
mientras que
 a-3b2c-4
a-3b2c-4
=
a-9b6c-12.
Luego, por las propiedades 3 y 4 se obtiene
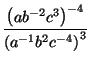
=
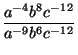
=
a9 - 4b8 - 6 =
a5b2.
Ejemplo 3.2.2
Resolver la siguiente ecuación:
2
. 4
n - 9
. 2
n + 4 = 0,
n 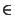 IZ
IZ.
Tomando
x = 2
n obtenemos la ecuación
2
x2 - 9
x + 4 = 0. Factorixando por
inspección, o usando la fórmula general, obtenemos las soluciones
x = 4,
x =

. Si
x = 4 obtenemos
2
n = 2
2, y no es difícil
convencerse de que esto implica
n = 2. Similarmente, si
x =

se
sigue que
n = - 1. El conjunto solución es entonces
S =

-1, 2
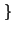
.
![]() IN. Para comenzar, si
queremos que la propiedad 1 sea válida con exponentes negativos, debemos
tener por ejemplo
IN. Para comenzar, si
queremos que la propiedad 1 sea válida con exponentes negativos, debemos
tener por ejemplo
![]() IZ. Por ejemplo,
nótese que
IZ. Por ejemplo,
nótese que
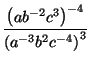 .
.
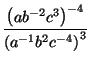 =
= 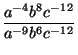 = a9 - 4b8 - 6 = a5b2.
= a9 - 4b8 - 6 = a5b2.