Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28 

Convergencia

Cuando los elementos an se acercan a cierto número real l, conforme n se hace grande, decimos que la sucesión $ \left(\vphantom{ a_{n}}\right.$an$ \left.\vphantom{ a_{n}}\right)$ converge a l. Para precisar esto mejor, tomamos un intervalo ]l - $ \varepsilon$, l + $ \varepsilon$[, con $ \varepsilon$ > 0. Si los an se acercan a l, debe tenerse an $ \in$ ]l - $ \varepsilon$, l + $ \varepsilon$[, para n suficientemente grande. Esto justifica la siguiente definición.

Definición 2.6.2   Decimos que la sucesión (an) converge a l $ \in$ IR si:

Para todo $ \varepsilon$ > 0 existe N $ \in$ IN tal que

| an - l| < $\displaystyle \varepsilon$,$\displaystyle \forall$n $\displaystyle \geq$ N.

En tal caso decimos que la sucesión (an) es convergente, y que su límite es l. Escribimos

$\displaystyle \lim_{n\rightarrow\infty}^{}$an = l.

También se usa la notación an $ \rightarrow$ l.

Si no existe tal l, decimos que (an) diverge.

Ejemplo 2.6.12   La sucesión constante (c) = $ \left(\vphantom{ c,c,c,\ldots}\right.$c, c, c,...$ \left.\vphantom{ c,c,c,\ldots}\right)$ converge a c. En efecto, como $ \left\vert\vphantom{ a_{n}-c}\right.$an - c$ \left.\vphantom{ a_{n}-c}\right\vert$ = 0 < $ \varepsilon$ para cada n, la definición de convergencia se cumple trivialmente.

Ejemplo 2.6.13   La sucesión $ \left(\vphantom{ \frac{1}{n}}\right.$$ {\frac{1}{n}}$$ \left.\vphantom{ \frac{1}{n}}\right)$ converge a l = 0.

Para ver esto, tomemos $ \varepsilon$ > 0. Debemos hallar N de manera que $ {\frac{1}{n}}$ < $ \varepsilon$ para todo n $ \geq$ N. Esto es equivalente a tener n > $ {\frac{1}{\varepsilon}}$, para n $ \geq$ N. Entonces basta tomar N = $ \left[\vphantom{ \frac{1}{\varepsilon}}\right.$$ {\frac{1}{\varepsilon}}$$ \left.\vphantom{ \frac{1}{\varepsilon}}\right]$ + 1, veamos:

n $\displaystyle \geq$ N $\displaystyle \Rightarrow$ n > $\displaystyle {\frac{1}{\varepsilon}}$ $\displaystyle \Rightarrow$ | an - 0| = $\displaystyle {\frac{1}{n}}$ < $\displaystyle \varepsilon$.

Ejemplo 2.6.14   La sucesión $ \left(\vphantom{ a_{n}}\right.$an$ \left.\vphantom{ a_{n}}\right)$ definida por an = $ {\frac{n^{2}%% -1}{n^{2}+1}}$ converge a l = 1. En efecto, dado $ \varepsilon$ > 0, veamos qué necesitamos para que $ \left\vert\vphantom{ a_{n}-1}\right.$an - 1$ \left.\vphantom{ a_{n}-1}\right\vert$ < $ \varepsilon$ :

$\displaystyle \left\vert\vphantom{ a_{n}-1}\right.$an - 1$\displaystyle \left.\vphantom{ a_{n}-1}\right\vert$ < $\displaystyle \varepsilon$ $\displaystyle \Leftrightarrow$ $\displaystyle \left\vert\vphantom{ \frac{n^{2}%% -1}{n^{2}+1}-1}\right.$$\displaystyle {\frac{n^{2}%% -1}{n^{2}+1}}$ - 1$\displaystyle \left.\vphantom{ \frac{n^{2}%% -1}{n^{2}+1}-1}\right\vert$ < $\displaystyle \varepsilon$ $\displaystyle \Leftrightarrow$ $\displaystyle {\frac{2}{n^{2}%% +1}}$ < $\displaystyle \varepsilon$ $\displaystyle \Leftrightarrow$ $\displaystyle {\frac{2}{\varepsilon}}$ < n2 + 1.

Para que esto ocurra basta que n2 > $ {\frac{2}{\varepsilon}}$, esto es n > $ \sqrt{\frac{2}{\varepsilon}}$. Entonces basta con tomar N = $ \left[\vphantom{ \sqrt{\frac{2}{\varepsilon}}}\right.$$ \sqrt{\frac{2}{\varepsilon}}$$ \left.\vphantom{ \sqrt{\frac{2}{\varepsilon}}}\right]$ + 1.

Ejemplo 2.6.15   La sucesión ((- 1)n) diverge. Para demostrar esto, supongamos lo contrario, y denotemos su límite por l. Tomando $ \varepsilon$ = 1 tendríamos la existencia de N tal que $ \left\vert\vphantom{ (-1)^{n}-l}\right.$(- 1)n - l$ \left.\vphantom{ (-1)^{n}-l}\right\vert$ < 1, para todo n $ \geq$ N. Pero para n par obtenemos l > 0, y para n impar obtenemos l < 0, lo cual es contradictorio.

El siguiente lema nos permite hablar de ``el límite'' de una sucesión.

Lema 2.6.1   Si (an) converge, su límite es único.

Prueba

Supongamos que l1 y l2 son límites de (an). Sea $ \varepsilon$ > 0. Por definición existen N1 y N2 tales que

| an - l1| < $ {\frac{\varepsilon}{2}}$,$ \forall$ n $ \geq$ N1,
| an - l2| < $ {\frac{\varepsilon}{2}}$,$ \forall$ n $ \geq$ N2.
Tomando n = max{N1, N2} se obtiene:

| l1 - l2| = | l1 - an + an - l2| $\displaystyle \leq$ | l1 - an| + | an - l2| < $\displaystyle \varepsilon$.

Concluimos entonces que | l1 - l2| < $ \varepsilon$ para cada $ \varepsilon$ > 0, con lo cual l1 = l2.

Otro resultado importante que resulta directo de la definición de lí mite es el siguiente:

Lema 2.6.2   Toda sucesión convergente es acotada.

Prueba

Consideremos una sucesión convergente $ \left(\vphantom{ a_{n}}\right.$an$ \left.\vphantom{ a_{n}}\right)$, y sea l su límite. Entonces tomando $ \varepsilon$ = 1, existe N $ \in$ IN tal que

| an| - | l| $\displaystyle \leq$ | an - l| < 1,$\displaystyle \forall$ n $\displaystyle \geq$ N.

Definiendo

M = max{| a1|,...,| aN - 1|,| l| + 1},

obtenemos | an| $ \leq$ M para todo n $ \in$ IN.

Nótese que el recíproco es falso, pues por ejemplo la sucesión ((- 1)n) es acotada y no convergente.

La demostración del siguiente lema la dejaremos como ejercicio:

Lema 2.6.3   Supongamos que (an) y (bn) son sucesiones convergentes, tales que para algún N $ \in$ IN se tiene

an $\displaystyle \leq$ bn,$\displaystyle \forall$ n $\displaystyle \geq$ N.

Entonces $ \lim\limits_{n\rightarrow\infty}^{}$an $ \leq$ $ \lim\limits_{n\rightarrow\infty}^{}$bn.

En particular, si para cada n se tiene an $ \geq$ 0, entonces $ \lim\limits_{n\rightarrow\infty}^{}$an $ \geq$ 0.

El siguiente resultado permite el cálculo y análisis de la convergencia de ciertas sucesiones, con base en otras más simples. Este resultado será central en la construcción de la función exponencial que expondremos luego.

Teorema 3 (Ley del emparedado)   Supongamos que las sucesiones (bn) y (cn) son convergentes a l, y que existe n0 tal que bn $ \leq$ an $ \leq$ cn,$ \forall$ n $ \geq$ n0. Entonces (an) también converge a l.

Prueba

Dado $ \varepsilon$ > 0, existe n1 $ \in$ IN tal que | bn - l| < $ \varepsilon$, $ \forall$ n $ \geq$ n1, y existe n2 tal que $ \left\vert\vphantom{ c_{n}-l}\right.$cn - l$ \left.\vphantom{ c_{n}-l}\right\vert$ < $ \varepsilon$, $ \forall$n $ \geq$ n2. Definiendo N = max$ \left\{\vphantom{ n_{0},n_{1},n_{2}}\right.$n0, n1, n2$ \left.\vphantom{ n_{0},n_{1},n_{2}}\right\}$ tenemos

l - $\displaystyle \varepsilon$ < bn $\displaystyle \leq$ an $\displaystyle \leq$ cn < l + $\displaystyle \varepsilon$,$\displaystyle \forall$ n $\displaystyle \geq$ N.

Por lo tanto (an) converge a l.

Ejemplo 2.6.16   La sucesión $ \left(\vphantom{ \frac{\left( -1\right) ^{n}}{n}}\right.$$ {\frac{\left( -1\right) ^{n}}{n}}$$ \left.\vphantom{ \frac{\left( -1\right) ^{n}}{n}}\right)$ converge a 0, pues - $ {\frac{1}{n}}$ $ \leq$ $ {\frac{\left( -1\right) ^{n}}{n}}$ $ \leq$ $ {\frac{1}{n}}$,$ \forall$ n $ \in$ IN.

Ejemplo 2.6.17   Considere la sucesión an = $ \sqrt[n]{2}$. Tomando $ \varepsilon_{n}^{}$ = $ \sqrt[n]{2}$ - 1 > 0, tenemos por la desigualdad de Bernoulli (ejercicio 3) que

2 = $\displaystyle \left(\vphantom{ \sqrt[n]{2}}\right.$$\displaystyle \sqrt[n]{2}$$\displaystyle \left.\vphantom{ \sqrt[n]{2}}\right)^{n}_{}$ = $\displaystyle \left(\vphantom{ 1+\varepsilon_{n}}\right.$1 + $\displaystyle \varepsilon_{n}^{}$$\displaystyle \left.\vphantom{ 1+\varepsilon_{n}}\right)^{n}_{}$ $\displaystyle \geq$ 1 + n$\displaystyle \varepsilon_{n}^{}$.

Esto muestra que

0 < $\displaystyle \varepsilon_{n}^{}$ $\displaystyle \leq$ $\displaystyle {\frac{1}{n}}$ $\displaystyle \rightarrow$ 0.

Por el teorema del emparedado se sigue que $ \varepsilon_{n}^{}$ $ \rightarrow$ 0, y consecuentemente an = $ \sqrt[n]{2}$ $ \rightarrow$ 1.

Si an $ \rightarrow$ l $ \neq$ 0, entonces eventualmente debe tenerse an $ \neq$ 0. Mejor aún, an se mantiene lejos de cero, para n grande. El siguiente lema expresa este hecho, de gran utilidad teórica.

Lema 2.6.4   Supongamos que an $ \rightarrow$ l $ \neq$ 0. Entonces existe n0 tal que para cada n $ \geq$ n0 se tiene $ \left\vert\vphantom{ a_{n}}\right.$an$ \left.\vphantom{ a_{n}}\right\vert$ > $ {\frac{1}{2}}$$ \left\vert\vphantom{ l}\right.$l$ \left.\vphantom{ l}\right\vert$.

Prueba

Basta tomar $ \varepsilon$ = $ {\frac{1}{2}}$$ \left\vert\vphantom{ l}\right.$l$ \left.\vphantom{ l}\right\vert$, el cual es positivo, y aplicar la definición de convergencia. Obtenemos la existencia de n0 tal que

l - $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \left\vert\vphantom{ l}\right.$l$\displaystyle \left.\vphantom{ l}\right\vert$ < an < l + $\displaystyle {\textstyle\frac{1}{2}}$$\displaystyle \left\vert\vphantom{ l}\right.$l$\displaystyle \left.\vphantom{ l}\right\vert$, $\displaystyle \forall$n $\displaystyle \geq$ n0.

Si l > 0 esto implica an > l - $ {\frac{1}{2}}$l = $ {\frac{1}{2}}$l. si por el contrario l < 0, se obtiene an < l + $ {\frac{1}{2}}$$ \left(\vphantom{ -l}\right.$ - l$ \left.\vphantom{ -l}\right)$ = $ {\frac{1}{2}}$l.

El cálculo de límites de sucesiones, se simplifica enormemente con el uso del siguiente teorema:

Teorema 4   Sean (an) y (bn) dos sucesiones convergentes, con an $ \rightarrow$ a y bn $ \rightarrow$ b, y sea c $ \in$ IR. Entonces:

  1. $ \lim\limits_{n\rightarrow\infty}^{}$c . an = c . a.

  2. $ \lim\limits_{n\rightarrow\infty}^{}$(c . an + bn) = c . a + b.

  3. $ \lim\limits_{n\rightarrow\infty}^{}$(an . bn) = a . b (ley del producto).

  4. Si bn $ \neq$ 0 para todo n, y si b $ \neq$ 0, entonces $ \lim\limits_{n\rightarrow\infty}^{}$$ {\frac{a_{n}}{b_{n}}}$ = $ {\frac{a}{b}}$ (ley del cociente).

Prueba

1.
Dado $ \varepsilon$ > 0, aplicamos la definición de convergencia de $ \left(\vphantom{ a_{n}}\right.$an$ \left.\vphantom{ a_{n}}\right)$, con $ {\frac{\varepsilon}{\left\vert c\right\vert +1}}$ en lugar de $ \varepsilon$, obteniendo que existe N tal que $ \left\vert\vphantom{ a_{n}-l}\right.$an - l$ \left.\vphantom{ a_{n}-l}\right\vert$ < $ {\frac{\varepsilon}{\left\vert c\right\vert +1}}$, para n $ \geq$ N. Luego

$\displaystyle \left\vert\vphantom{ c\cdot a_{n}-c\cdot a}\right.$c . an - c . a$\displaystyle \left.\vphantom{ c\cdot a_{n}-c\cdot a}\right\vert$ = $\displaystyle \left\vert\vphantom{ c}\right.$c$\displaystyle \left.\vphantom{ c}\right\vert$ . $\displaystyle \left\vert\vphantom{ a_{n}-l}\right.$an - l$\displaystyle \left.\vphantom{ a_{n}-l}\right\vert$ $\displaystyle \leq$ $\displaystyle \left\vert\vphantom{ c}\right.$c$\displaystyle \left.\vphantom{ c}\right\vert$ . $\displaystyle {\frac{\varepsilon}{\left\vert c\right\vert +1}}$ < $\displaystyle \varepsilon$, $\displaystyle \forall$n $\displaystyle \geq$ N.

2.
Dado $ \varepsilon$ > 0, existen n0 y n1 tales que

$\displaystyle \left\vert\vphantom{ a_{n}-a}\right.$an - a$\displaystyle \left.\vphantom{ a_{n}-a}\right\vert$ < $\displaystyle {\frac{\varepsilon}{2}}$, $\displaystyle \forall$n $\displaystyle \geq$ n0;  $\displaystyle \left\vert\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right\vert$ < $\displaystyle {\frac{\varepsilon}{2}}$, $\displaystyle \forall$n $\displaystyle \geq$ n1.

Tomando N = max$ \left(\vphantom{ n_{0},n_{1}}\right.$n0, n1$ \left.\vphantom{ n_{0},n_{1}}\right)$ obtenemos que

$\displaystyle \left\vert\vphantom{ \left( a_{n}+b_{n}\right) -\left( a+b\right) }\right.$$\displaystyle \left(\vphantom{ a_{n}+b_{n}}\right.$an + bn$\displaystyle \left.\vphantom{ a_{n}+b_{n}}\right)$ - $\displaystyle \left(\vphantom{ a+b}\right.$a + b$\displaystyle \left.\vphantom{ a+b}\right)$$\displaystyle \left.\vphantom{ \left( a_{n}+b_{n}\right) -\left( a+b\right) }\right\vert$ = $\displaystyle \left\vert\vphantom{ \left( a_{n}-a\right) +\left( b_{n}-b\right) }\right.$$\displaystyle \left(\vphantom{ a_{n}-a}\right.$an - a$\displaystyle \left.\vphantom{ a_{n}-a}\right)$ + $\displaystyle \left(\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right)$$\displaystyle \left.\vphantom{ \left( a_{n}-a\right) +\left( b_{n}-b\right) }\right\vert$ $\displaystyle \leq$ $\displaystyle \left\vert\vphantom{ a_{n}-a}\right.$an - a$\displaystyle \left.\vphantom{ a_{n}-a}\right\vert$ + $\displaystyle \left\vert\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right\vert$ < $\displaystyle \varepsilon$, $\displaystyle \forall$n $\displaystyle \geq$ N.

Esto demuestra que an + bn $ \rightarrow$ a + b. Además, por la parte 1 tenemos que c . an $ \rightarrow$ c . a, y por lo que acabamos de demostrar se obtiene que c . an + bn $ \rightarrow$ c . a + b.

3.
Como (bn) es convergente, se sigue que es acotada, y entonces existe T > 0 tal que | bn| $ \leq$ T, $ \forall$ n $ \in$ IN. Además

| anbn - ab| = $\displaystyle \left\vert\vphantom{ \left( a_{n}-a\right) b_{n}+a\left( b_{n}-b\right) }\right.$$\displaystyle \left(\vphantom{ a_{n}-a}\right.$an - a$\displaystyle \left.\vphantom{ a_{n}-a}\right)$bn + a$\displaystyle \left(\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right)$$\displaystyle \left.\vphantom{ \left( a_{n}-a\right) b_{n}+a\left( b_{n}-b\right) }\right\vert$ $\displaystyle \leq$ | an - a|| bn| + | a|| bn - b|,

y por lo tanto

| anbn - ab| $\displaystyle \leq$ T$\displaystyle \left\vert\vphantom{ a_{n}-a}\right.$an - a$\displaystyle \left.\vphantom{ a_{n}-a}\right\vert$ + | a|$\displaystyle \left\vert\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right\vert$. 

Como $ \left\vert\vphantom{ a_{n}-a}\right.$an - a$ \left.\vphantom{ a_{n}-a}\right\vert$ $ \rightarrow$ 0 y $ \left\vert\vphantom{ b_{n}-b}\right.$bn - b$ \left.\vphantom{ b_{n}-b}\right\vert$ $ \rightarrow$ 0, las propiedades anteriores permiten concluir que

T$\displaystyle \left\vert\vphantom{ a_{n}-a}\right.$an - a$\displaystyle \left.\vphantom{ a_{n}-a}\right\vert$ + | a|$\displaystyle \left\vert\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right\vert$ $\displaystyle \rightarrow$ 0.

Por el teorema del emparedado concluimos que

$\displaystyle \lim\limits_{n\rightarrow\infty}^{}$| anbn - ab| = 0. 

3.
Por el lema anterior, existe n0 tal que | bn| > $ {\frac{1}{2}}$| b|, $ \forall$n $ \geq$ n0. Luego

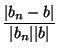$\displaystyle \left\vert\vphantom{ \frac{1}{b_{n}}-\frac{1}{b}}\right.$$\displaystyle {\frac{1}{b_{n}}}$ - $\displaystyle {\frac{1}{b}}$$\displaystyle \left.\vphantom{ \frac{1}{b_{n}}-\frac{1}{b}}\right\vert$ = $\displaystyle {\frac{\vert b_{n}-b\vert}{\vert b_{n}%% \vert\vert b\vert}}$ < $\displaystyle {\frac{2}{b^{2}}}$$\displaystyle \left\vert\vphantom{ b_{n}-b}\right.$bn - b$\displaystyle \left.\vphantom{ b_{n}-b}\right\vert$,  $\displaystyle \forall$n $\displaystyle \geq$ n0.

Por la propiedad 1 y el teorema del emparedado concluimos que

$\displaystyle \left\vert\vphantom{ \frac{1}{b_{n}}-\frac{1}{b}}\right.$$\displaystyle {\frac{1}{b_{n}}}$ - $\displaystyle {\frac{1}{b}}$$\displaystyle \left.\vphantom{ \frac{1}{b_{n}}-\frac{1}{b}}\right\vert$ $\displaystyle \rightarrow$ 0.

Combinando con la propiedad 2, obtenemos

$\displaystyle {\frac{a_{n}}{b_{n}}}$ = an . $\displaystyle {\frac{1}{b_{n}}}$ $\displaystyle \rightarrow$ a . $\displaystyle {\frac{1}{b}}$ = $\displaystyle {\frac{a}{b}}$.

Ejemplo 2.6.18   Sea an = $ {\frac{1}{n^{2}}}$. Como $ {\frac{1}{n}}$ $ \rightarrow$ 0, tenemos que $ {\frac{1}{n^{2}}}$ = $ {\frac{1}{n}}$ . $ {\frac{1}{n}}$ $ \rightarrow$ 0, por la ley del producto.

Ejemplo 2.6.19   Si an = 1 + $ {\frac{3}{n}}$ - $ {\frac{5}{n^{2}}}$ tenemos que an $ \rightarrow$ 1, por el ejemplo anterior, y las propiedades 1, 2 y 4.

Ejemplo 2.6.20   Si an = $ {\frac{n}{n^{2}+1}}$ tenemos an = $ {\frac{1}{n}}$ . $ {\frac{1}{1+\frac{1}{n^{2}}}}$ $ \rightarrow$ 0 . $ {\frac{1}{1+0}}$ = 0.

Ejemplo 2.6.21   Sea an = $ {\frac{n^{2}+3n-5}{2n^{2}+40n+6}}$. Factorizando n2 tenemos

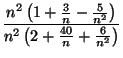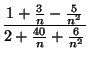
an = $\displaystyle {\frac{n^{2}\left( 1+\frac{3}{n}-\frac{5}{n^{2}}\right) }{n^{2}\left( 2+\frac{40}{n}+\frac{6}{n^{2}}\right) }}$ = $\displaystyle {\frac{1+\frac{3}{n}-\frac{5}{n^{2}}%% }{2+\frac{40}{n}+\frac{6}{n^{2}}}}$ $\displaystyle \rightarrow$ $\displaystyle {\textstyle\frac{1}{2}}$.

Ejemplo 2.6.22   Considere la sucesión an = $ \sqrt[n]{a}$, donde a > 1 es fijo. Tomando $ \varepsilon_{n}^{}$ = $ \sqrt[n]{a}$ - 1 > 0, tenemos por la desigualdad de Bernoulli (ejercicio 3) que

a = $\displaystyle \left(\vphantom{ \sqrt[n]{a}}\right.$$\displaystyle \sqrt[n]{a}$$\displaystyle \left.\vphantom{ \sqrt[n]{a}}\right)^{n}_{}$ = $\displaystyle \left(\vphantom{ 1+\varepsilon_{n}}\right.$1 + $\displaystyle \varepsilon_{n}^{}$$\displaystyle \left.\vphantom{ 1+\varepsilon_{n}}\right)^{n}_{}$ $\displaystyle \geq$ 1 + n$\displaystyle \varepsilon_{n}^{}$ > n$\displaystyle \varepsilon_{n}^{}$

Esto demuestra que

0 < $\displaystyle \varepsilon_{n}^{}$ $\displaystyle \leq$ $\displaystyle {\frac{a}{n}}$, para cada n $\displaystyle \geq$ 1.

Por la propiedad 1 del teorema anterior se tiene que $ {\frac{a}{n}}$ $ \rightarrow$ 0, y por el teorema del emparedado se concluye que $ \varepsilon_{n}^{}$ $ \rightarrow$ 0. Consecuentemente, por la propiedad 2 del teorema anterior se concluye:

an = $\displaystyle \sqrt[n]{a}$ = 1 + $\displaystyle \varepsilon_{n}^{}$ $\displaystyle \rightarrow$ 1.

Ejemplo 2.6.23   Si an = $ {\frac{n+\cos n}{3n+1}}$ tenemos

$\displaystyle {\frac{n-1}{3n+1}}$ $\displaystyle \leq$ an $\displaystyle \leq$ $\displaystyle {\frac{n+1}{3n+1}}$.

Además

$\displaystyle {\frac{n+1}{3n+1}}$ = $\displaystyle {\frac{1+\frac{1}{n}}{3+\frac{1}{n}}}$ $\displaystyle \rightarrow$ $\displaystyle {\textstyle\frac{1}{3}}$,        $\displaystyle {\frac{n-1}{3n+1}}$ = $\displaystyle {\frac{1-\frac{1}{n}}{3+\frac{1}{n}}}$ $\displaystyle \rightarrow$ $\displaystyle {\textstyle\frac{1}{3}}$.

Por el teorema del emparedado obtenemos que an $ \rightarrow$ $ {\frac{1}{3}}$.

El siguiente teorema será la base en la construcción de la función exponencial que haremos luego.

Teorema 5 (Weierstrass)   Toda sucesión monótona y acotada es convergente.

Prueba

Sea (an) acotada y creciente. Sea l = sup{an : n $ \in$ IN}, y sea $ \varepsilon$ > 0. Por definición de supremo (o el teorema 1) existe N $ \in$ IN tal que aN > l - $ \varepsilon$. Como $ \left(\vphantom{ a_{n}}\right.$an$ \left.\vphantom{ a_{n}}\right)$ es creciente se sigue que

l - $\displaystyle \varepsilon$ < aN $\displaystyle \leq$ an $\displaystyle \leq$ l, $\displaystyle \forall$n $\displaystyle \geq$ N.

Esto demuestra que an $ \rightarrow$ l. El caso decreciente se trata de manera similar.

Ejemplo 2.6.24   Considere la sucesión dada recurrentemente por:

a0 = $\displaystyle \sqrt{2}$,  an = $\displaystyle \sqrt{2+a_{n-1}}$,   para n $\displaystyle \geq$ 1.

Los términos de esta sucesión son

$\displaystyle \sqrt{2}$,$\displaystyle \sqrt{2+\sqrt{2}}$,$\displaystyle \sqrt{2+\sqrt{2+\sqrt{2}}}$,....

Veremos que (an) es creciente y acotada superiormente. Para esto probaremos, usando el principio de inducción, que para todo n $ \in$ IN se tiene an $ \leq$ an + 1 $ \leq$ 2.

  • Para n = 0: a0 = $ \sqrt{2}$ $ \leq$ a1 = $ \sqrt{2+\sqrt{2}}$ $ \leq$ $ \sqrt{2+2}$ = 2.

  • Paso inductivo: Si an $ \leq$ an + 1 $ \leq$ 2, se sigue que 2 + an $ \leq$ 2 + an + 1 $ \leq$ 2 + 2 = 4, y entonces

    $\displaystyle \sqrt{2+a_{n}}$ $\displaystyle \leq$ $\displaystyle \sqrt{2+a_{n+1}}$ $\displaystyle \leq$ 2,

    esto es an + 1 $ \leq$ an + 2 $ \leq$ 2.

Luego, por el teorema de Weierstrass tenemos que existe l $ \in$ IR tal que an $ \rightarrow$ l. Pero por las propiedades de los límites se debe tener

l = $\displaystyle \lim\limits_{n\rightarrow\infty}^{}$an + 1 = $\displaystyle \lim\limits_{n\rightarrow\infty}^{}$$\displaystyle \sqrt{2+a_{n}}$ = $\displaystyle \sqrt{2+l}$,

y entonces l2 - l - 2 = 0. Esto demuestra que l = - 1 ó l = 2, pero como l es positivo, se concluye que l = 2. Hemos demostrado que

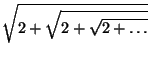$\displaystyle \sqrt{2+\sqrt{2+\sqrt{2+\ldots}}}$ = 2.

Note que el teorema de Weierstrass es imprescindible en este ejemplo, ya que la manipulación para hallar l solo está justificada después de conocer su existencia.

  Inicio  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28